链接
24. 两两交换链表中的节点
19.删除链表的倒数第N个节点
面试题 02.07. 链表相交
142.环形链表II
链表总结篇
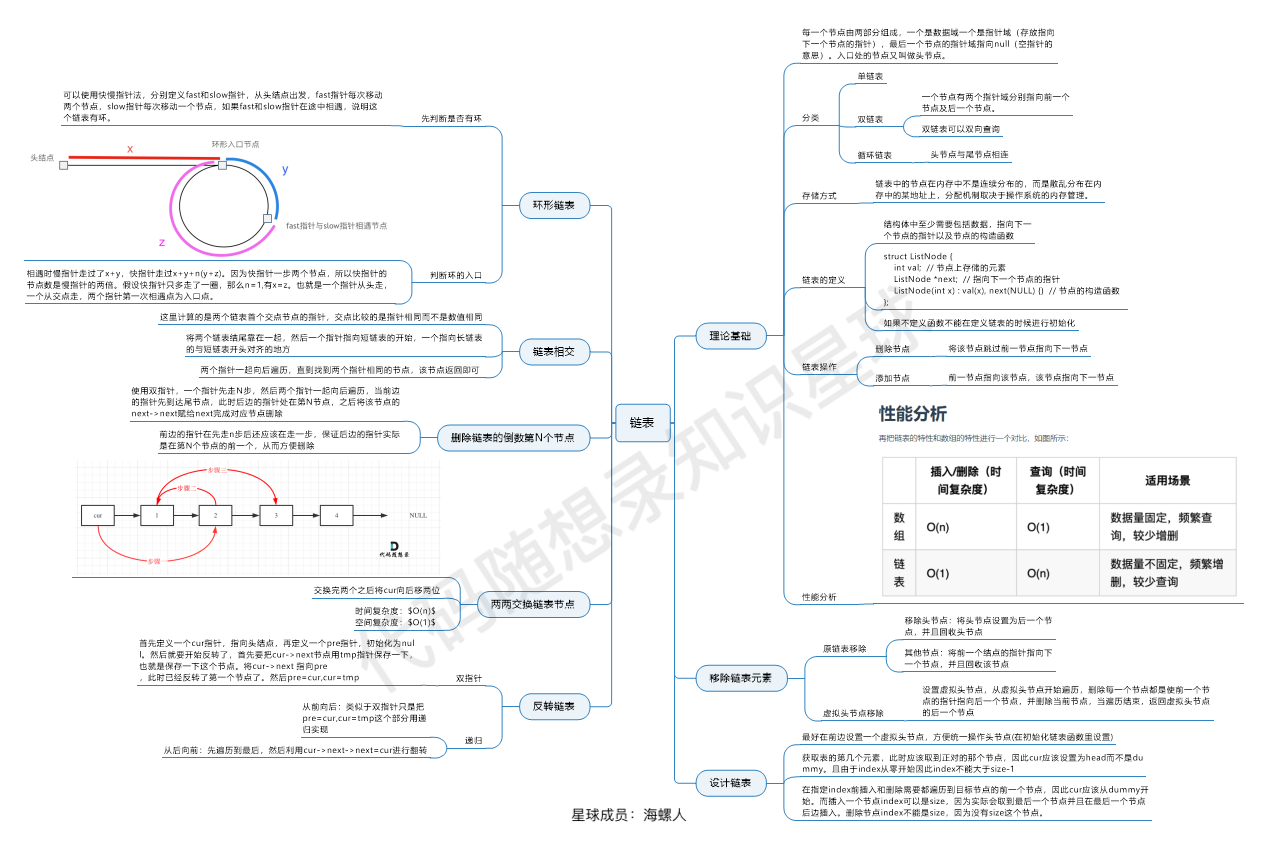
知识
面试题 02.07. 链表相交
- 两个链表的交点不是数值相等,而是指针相等。
- 本题在构造测试样例时,会输入两个单链表和两个单链表的交叉点,以及交叉点到两个链表头节点的距离。因此,只有指定的交叉点才是真正的交叉点,仅仅是值相等的节点并不一定是真正的交叉点。指定的交叉点被构造出来时在内存中的地址相同,而仅仅是值相等的两个节点在内存中的地址不一定相同。
初次尝试
24. 两两交换链表中的节点
应该和交换数组中的两个元素相同。需要创建一个额外的节点tmp,然后若要交换a节点和b节点,则进行:tmp = b, a = b, b = tmp即可。
19.删除链表的倒数第N个节点
我能想到的办法:先遍历一遍列表,返回列表有几个节点。然后再遍历一遍列表,当cur指向倒数第N个节点的前一个节点时,停止遍历链表,删除cur->next,然后返回链表的头节点即可。应该也要用到虚拟头节点,避免删除链表的第一个节点时需要特判。我按照上述思路写了代码,可以成功通过测评!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
int size = 0;
ListNode* cur = dummyHead;
while (cur->next != NULL)
{
cur = cur->next;
size ++ ;
}
ListNode* cur1 = dummyHead;
int size1 = 0;
while (size1 < size - n)
{
cur1 = cur1->next;
size1 ++ ;
}
ListNode* tmp = cur1->next;
cur1->next= cur1->next->next;
delete tmp;
return dummyHead->next;
}
};
|
更好的办法是采用双指针算法,见实现部分。
面试题 02.07. 链表相交
我的第一想法是采用暴力解法。一个指针指向链表A的头节点,一个指针指向链表B的头节点,移动两个指针,当两个指针指向同一个节点时,说明该节点是两个链表相交的节点。据此,我写出了暴力解法的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* dummyHead1 = new ListNode(0);
ListNode* dummyHead2 = new ListNode(0);
dummyHead1->next = headA;
dummyHead2->next = headB;
ListNode* cur1 = dummyHead1;
ListNode* cur2 = dummyHead2;
for (cur1 = dummyHead1; cur1 != NULL; cur1 = cur1->next)
{
for (cur2 = dummyHead2; cur2 != NULL; cur2 = cur2->next)
{
if (cur1 == cur2)
return cur1;
}
}
return NULL;
}
};
|
暴力解法的时间复杂度是O(n^2),应该有时间复杂度为O(n)的解法。时间复杂度更低的代码参见代码随想录。
142.环形链表II
从没有见过这类题目,拿到题目毫无思路,直接看视频讲解和文字题解。
实现
24. 两两交换链表中的节点
注意:是交换链表中的节点,而不仅仅交换节点的数值。偶数个节点则正好两两交换,奇数个节点则最后一个点不参与交换。一定需要dummyHead,因为要交换节点1、2,就一定要用到它们之前的那个节点,即dummyHead(dummyHead->2->1->3->…)。同理,要交换节点3、4,就一定要用到它们之前的那个节点,即节点2。因此当前指针一定要指向要反转的两个节点中的前一个节点,且当前指针每次移动两位。
若链表中的节点个数为奇数,则cur->next->next == NULL时循环结束,若链表中的节点个数为偶数,则cur -> next == NULL时循环结束。如下图所示。故遍历结束的条件为 while (cur->next != NULL && cur->next->next != NULL)。两个条件不可以反过来写,否则当出现空链表时,cur->next->next没有被定义,会出现空指针异常。
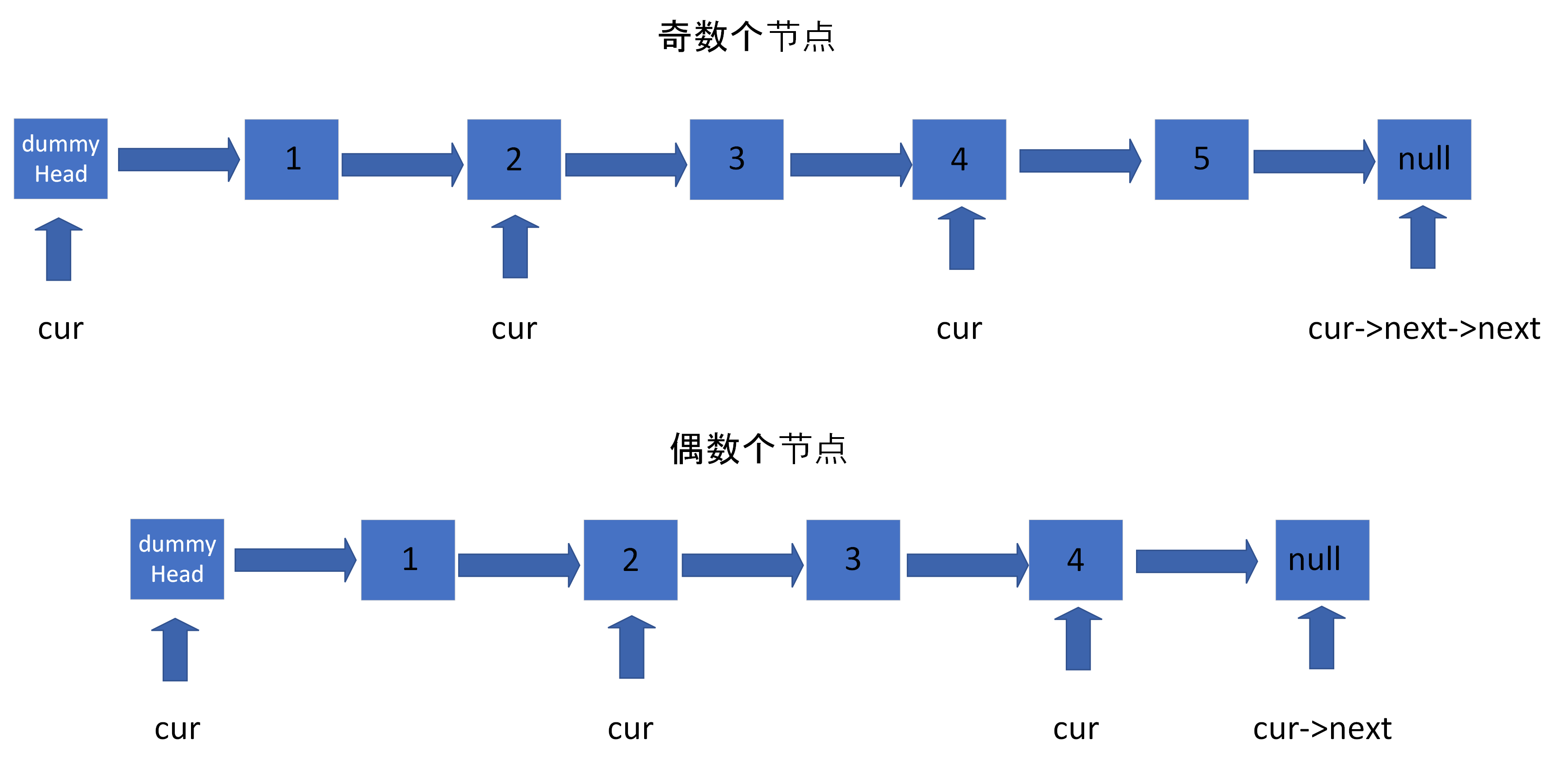
接下来是两两交换节点的逻辑。改变后的链表为dummyHead->2->1->3,由于dummyHead->1改变为dummyHead->2后,原本的节点1已经不能被访问到了,因此需要先用tmp存下节点1。同理,由于要将2->3改为2->1,因此需要先用tmp1存下节点3。交换完节点的链表为:dummyHead->2->1->4->3…..。对于两两交换节点的逻辑,可以参考代码随想录教程中的三幅图片。

交换3和4节点的步骤时:cur目前为1,我们让1指向4,4再指向3,3再指向5(如果有5的话)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* cur = dummyHead;
while (cur->next != NULL && cur->next->next != NULL)
{
ListNode* tmp = cur->next;
ListNode* tmp1 = cur->next->next->next;
cur->next = cur->next->next;
cur->next->next = tmp;
tmp->next = tmp1;
cur = cur->next->next;
}
return dummyHead->next;
}
};
|
19.删除链表的倒数第N个节点
看了代码随想录的思路之后,我独立写出了快慢指针解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* fast = dummyHead;
ListNode* slow = dummyHead;
while (n -- ) fast = fast->next;
while (fast->next != NULL)
{
slow = slow->next;
fast = fast->next;
}
ListNode* tmp = slow->next;
slow->next = slow->next->next;
delete tmp;
return dummyHead->next;
}
};
|
也可以让fast先向后移动(n + 1)位,然后让fast和slow同时移动,直到fast移动到NULL为止,此时slow指向的也是倒数第n个节点的前一个节点。对这种办法,可以在移动fast指针前先让n ++ , 也可以在第一个while循环后让fast指针多向后移动一位。最稳妥的写法如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* fast = dummyHead;
ListNode* slow = dummyHead;
n ++ ;
while (n -- && fast != NULL) fast = fast->next;
while (fast != NULL)
{
fast = fast->next;
slow = slow->next;
}
ListNode* tmp = slow->next;
slow->next = slow->next->next;
delete tmp;
return dummyHead->next;
}
};
|
由于题目有如下限制:
1
2
3
4
| The number of nodes in the list is sz.
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz
|
因此即使不加上fast != NULL,也可以通过,但如果题目没有n <= sz的限制,那么必须加上fast != NULL,且不能使用以下写法:
1
2
| while (n -- && fast != NULL) fast = fast->next;
fast = fast->next;
|
因为若采用以上写法,当n > sz时,当while循环结束后,fast已经指向了NULL,此时再做fast = fast->next操作,会导致空指针异常。
面试题 02.07. 链表相交
代码随想录的思路:求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB末尾对齐的位置。此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点。否则循环退出返回空指针。
看了代码随想录的思路后,我独立写出了代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int sizea = 0, sizeb = 0;
ListNode* cura = headA;
ListNode* curb = headB;
while (cura != NULL)
{
cura = cura->next;
sizea ++ ;
}
while (curb != NULL)
{
curb = curb->next;
sizeb ++ ;
}
cura = headA, curb = headB;
int delta = abs(sizea - sizeb);
if (sizea >= sizeb)
{
while (delta -- ) cura = cura->next;
while (sizeb -- )
{
if (cura == curb) return cura;
else
{
cura = cura->next;
curb = curb->next;
}
}
}
else
{
while (delta -- ) curb = curb->next;
while (sizea -- )
{
if (cura == curb) return cura;
else
{
cura = cura->next;
curb = curb->next;
}
}
}
return NULL;
}
};
|
这里特别需要注意的是,在计算完a链表和b链表的长度后,需要让 cura = headA, curb = headB。
代码随想录的写法更见简洁:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* cura = headA, * curb = headB;
int sizea = 0, sizeb = 0;
while (cura != NULL)
{
cura = cura->next;
sizea ++ ;
}
while (curb != NULL)
{
curb = curb->next;
sizeb ++ ;
}
if (sizea < sizeb)
{
swap(sizea, sizeb);
swap(headA, headB);
}
cura = headA, curb = headB;
int delta = sizea - sizeb;
while (delta -- ) cura = cura->next;
while (cura != NULL)
{
if (cura == curb) return cura;
cura = cura->next;
curb = curb->next;
}
return NULL;
}
};
|
142.环形链表II
有两问:
判断链表中是否有环
用快慢指针来判断是否有环。若链表是一条直线,则快慢指针永远不会相遇。只有当链表中有环存在时,快指针先进入了环且在环中浪费了时间,快慢指针才会相遇。快指针从头节点开始,每次移动两位,慢指针也从头节点开始,每次移动一位,二者若相遇则一定在环里相遇,相遇则说明有环。快指针是一个节点一个节点的靠近慢指针,因此二者一定会在环中相遇。
找到环的入口
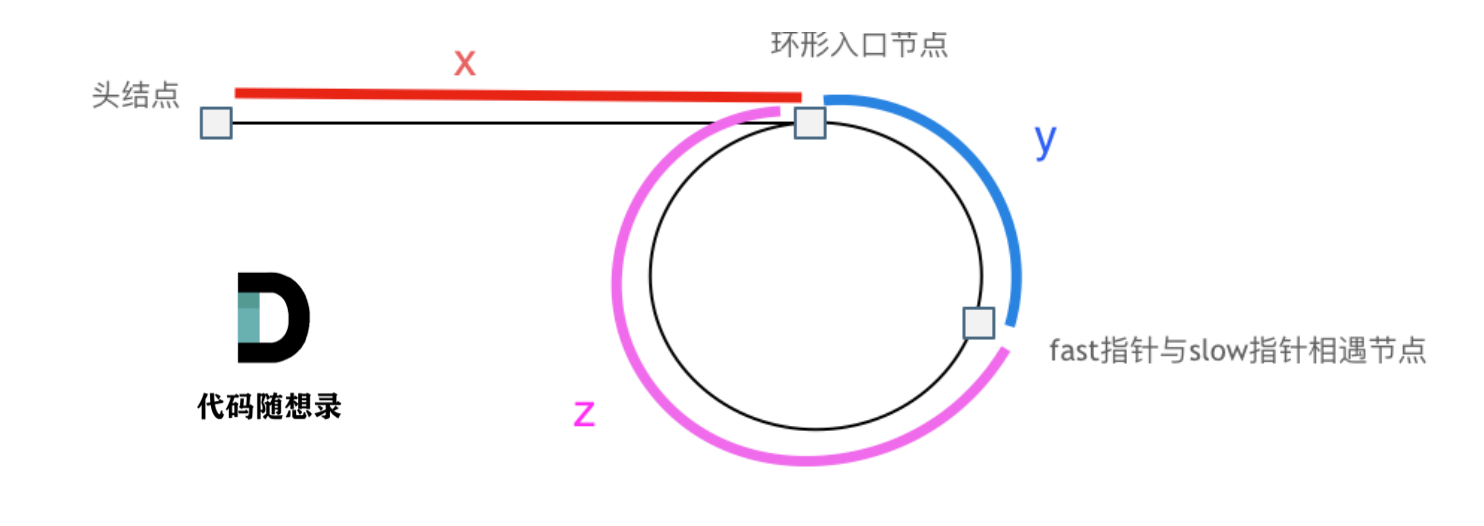
列方程即可解出x:x = n (y + z) - y, (n >= 1),由于看不出x和负数-y之间的关系,我们让出一圈,看x和z的关系:x = (n - 1) (y + z) + z, (n >= 1)。这就意味着:从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是环形入口的节点。
为什么第一次在环中相遇,slow的步数是x+y而不是 x + 若干环的长度 + y 呢?”这个问题,可以这样解释,设快指针每秒移动2格,慢指针每秒移动1格,圆的周长是k。则慢指针走一圈需要的时间是k,设两指针之间的距离为m(m < k),则快指针追上慢指针的时间是m(快指针相对于满指针每秒移动1格),此时慢指针走过的距离是m,由于m < k,因此慢指针在遇到快指针之前走过的距离小于圆的周长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head, * slow = head;
while (fast != NULL && fast->next != NULL)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
{
ListNode* index1 = fast, * index2 = head;
while (index1 != index2)
{
index1 = index1->next;
index2 = index2->next;
}
return index1;
}
}
return NULL;
}
};
|
我自研的另一种写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head, * slow = head;
bool flag = false;
while (fast != NULL && fast->next != NULL)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
{
flag = true;
break;
}
}
if (flag && fast == slow)
{
ListNode* index1 = head, * index2 = slow;
while(index1 != index2)
{
index1 = index1->next;
index2 = index2->next;
}
return index1;
}
else
return NULL;
}
};
|
注意,一定要通过flag判断,只有当fast和slow相等且二者都在第一个while循环中转过时,才能确保链表中有环,若fast和slow相等,则可能是链表中只有一个节点的情况,此时fast和slow都没有在第一个循环中转过,因此二者相等且都等于head。
心得与备忘录
24. 两两交换链表中的节点
- 注意cur应该指向哪里。
- 注意遍历的终止条件(奇数/偶数个节点)
- 若原先的两节点之间的连接被断开,则需要在断开前保存两节点中后面那个节点,否则后面的那个节点无法被访问到
面试题 02.07. 链表相交
- 本题的关键思路在于:对齐两个链表的尾部。本题的算法实际上也是(快慢)双指针算法。
- 比较链表中的两个节点是否相同,直接用
cura == curb即可,不能用 cura->val == curb->val && cura->next == curb->next,因为比较两个节点除去比较val和next这两个参数外,还需要比较其本身的内存地址。
- 本题的时间复杂度分析:
计算两个链表的长度:O(n) + O(m)
调整指针以对齐两个链表:O(n - m)或O(m - n)
同时遍历两个链表寻找交点:O(min(n, m))
第一步和第三步的时间复杂度加在一起是 O(n) + O(m) + O(min(n, m))。但是,因为 O(min(n, m))在 O(n) + O(m)中已经被包含(总是小于或等于 n和 m),所以总的时间复杂度简化为 O(n) + O(m)。第二步(调整指针以对齐两个链表)的时间复杂度实际上也包含在 O(n) + O(m)中,因为无论是 n - m还是 m - n,它的值总是小于或等于 n和 m。因此,整个函数的总时间复杂度为 O(n + m),这里 n和 m分别是两个链表的长度。这个时间复杂度已经涵盖了所有的主要操作,包括计算长度、对齐链表和寻找交点。时间复杂度的计算应当关注主要操作,省略次要操作。
- 在leetcode中调用swap,abs等函数时,不需要自行引用头文件,基本的函数和数据结构(STL)已经默认被引用了,因此直接写出来即可。
142.环形链表II
- 记住使用快慢双指针算法,有环的情况下快慢指针必然会相遇。
- 画图理解如何求环的起点的index。
- 记得复习时着重看这道题
总结:链表
- 插入虚拟头节点dummyHead,可以避免空链表并避免对头节点操作的特判
- 创建一个当前节点cur,对整个链表进行遍历(
cur = cur->next),而不用链表中原本存在的节点对链表进行遍历
- NULL节点表示不存在的节点;虚拟节点实际上是存在的,其值为0,是人为创建的节点
- 递归时,需要先检查递归的终止条件,然后执行递归步骤
- 想要删除哪个节点,就用cur指针指向其前面的那个节点
- 链表中最常用的算法是双指针算法,在206.反转链表,19.删除链表的倒数第N个节点,面试题 02.07. 链表相交,142.环形链表II中都用到了,其他题目基本不需要算法,利用链表的一些基本性质进行增删改查即可。
- 记得复习142.环形链表II和24.两两交换链表中的节点,前者是链表中最独特也最难的一道题,难在数学推导和想清楚细节;后者在退出循环的条件和用tmp保存节点方面需要特别注意。