Day 17 | Leetcode 110, 257, 404

链接

知识

257. 二叉树的所有路径

404.左叶子之和

初次尝试

110.平衡二叉树

先尝试递归解法。我写下了如下的代码，可以运行成功，但时间复杂度较高：

class Solution {
public:
    // 求最大根节点的最大高度，用后序遍历
    int getheight(TreeNode* node)
    {
        if (node == NULL) return 0;
        int left = getheight(node->left);
        int right = getheight(node->right);
        int res = 1 + max(left, right);
        return res;
    }

    bool isBalanced(TreeNode* root) {
        if (root == NULL) return true;

        bool left = isBalanced(root->left);
        int leftdepth = getheight(root->left);

        bool right = isBalanced(root->right);
        int rightdepth = getheight(root->right);

        bool flag = false;
        if (abs(leftdepth - rightdepth) <= 1) flag = true;

        // 根节点需要同时满足：左子树为平衡二叉树，右子树也为平衡二叉树，且左右子树高度差<=1
        // 整个树才是平衡二叉树
        bool res = left && right && flag;
        return res;
    }
};

接着看卡尔的讲解。

257. 二叉树的所有路径

拿到本题，我毫无办法，直接看卡尔的讲解。

404.左叶子之和

本题我本来想一上来就是层序遍历，但后面发现是左叶子，而非左孩子。叶子节点是没有左右孩子的节点。我产生了一个另外的想法，先前序遍历一遍二叉树，遍历到左节点时判断左节点是否是左叶子节点，是的话则将其加入结果res中，最后返回res即可。我尝试了，但做不出来，看卡尔的讲解。

实现

110.平衡二叉树

平衡二叉树：二叉树中任何一个节点左右子树的高度差不超过1。求高度要用后序遍历。本题可以用递归法，也可以用迭代法，但优先掌握递归法。

int getHeight(TreeNode* node) // 返回一个节点的高度
{
    if (node == NULL) return 0; // 终止条件
    
    // 后序遍历
    // 若某节点的左右子树的高度差超过1，说明该子树不再为平衡二叉树，进而说明整个树并非平衡二叉树
    // 当发现这样的节点时，就不返回节点的高度，直接返回-1
    // 左
    int left = getHeight(node->left);
    if (left == -1) return -1; // 左子树并非平衡二叉树，则返回-1
    // 右
    int right = getHeight(node->right);
    if (right == -1) return -1; // 右子树并非平衡二叉树，则返回-1
    
    // 中
    int res;
    if (abs(left - right) > 1) res = -1; // 左右子树相差大于1，则说明该子树为非平衡二叉树，返回-1
    else res = 1 + max(left, right); // 计算左右子树的父节点的高度
    return res;
}

必须用后序遍历，因为需要先计算左右子树的高度，然后才能进行比较。完整代码如下所示：

class Solution {
public:
    // node为根节点的二叉树是平衡二叉树则返回node的高度，是非平衡二叉树则返回-1
    int getheight(TreeNode* node)
    {
        if (node == NULL) return 0;

        int left = getheight(node->left);
        if (left == -1) return -1;
        int right = getheight(node->right);
        if (right == -1) return -1;

        int res;
        if (abs(left - right) > 1) res = -1;
        else res = 1 + max(left, right);
        return res;
    }
    bool isBalanced(TreeNode* root) {
        if (getheight(root) == -1) return false;
        return true;
    }
};

257. 二叉树的所有路径

给定二叉树，返回从根节点到叶子节点的所有路径。求路径需要使用前序遍历。原因：只有前序遍历可以让父节点指向孩子节点，从而输出路径。虽然也可以用迭代法，但推荐使用递归法。回溯和递归是相辅相成、相伴而生的。本题第一次提到回溯。本题的解题过程中有回溯的过程。

为什么会有回溯？假设有以下的二叉树：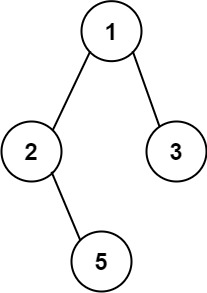

假设有容器收集路径，收集到路径125，如何弹出2和5，然后再让容器重新收集路径13？回溯的过程：弹出5和2，加入3。
关键代码：

// path数组用来记录单条路径
// res数组用来存放最终的结果（包含多条路径），是一个数组，数组的每个元素都是一个字符串
void traversal(TreeNode* node, vector<int>& path, vector<string>& res)
{
    path.push_back(node->val); // 中：处理过程
    
    // 终止条件
    // 左右孩子都为空，说明遍历到了叶子节点，收获结果
    if (node->left == NULL && node->right == NULL) 
    {
        res.push_back(path); // 将单条路径的结果放入最终结果中，省略了vector->string和加上->的代码
        return;
    }
    
    // 单层处理逻辑，用前序遍历：中左右
    // 中：处理过程，即添加遍历到的节点，本题的处理过程需要写到终止条件之前
    // 因为本题的终止条件是到叶子节点，若中写在终止条件之后，则叶子节点没有被放入path中
    // 左
    if (node->left) 
    {
        traversal(node->left, path, res); 
    	  path.pop_back(); // 回溯，弹出5和2
    }
    // 右
    if (node->right) 
    {
        traversal(node->right, path, res);
    	  path.pop_back(); // 回溯
    }
}

完整的代码：

class Solution {
public:
    void traversal(TreeNode* node, vector<int>& path, vector<string>& res)
    {
        path.push_back(node->val); // 中

        // 终止条件
        if (node->left == NULL && node->right == NULL)
        {
            string s;
            for (int i = 0; i < path.size() - 1; i ++ )
            {
                s += to_string(path[i]);
                s += "->";
            }
            s += to_string(path[path.size() - 1]);
            res.push_back(s);
            return;
        }

        // 左
        if (node->left) 
        {
            traversal(node->left, path, res);
            path.pop_back(); // 回溯
        }
        // 右
        if (node->right) 
        {
            traversal(node->right, path, res);
            path.pop_back(); // 回溯
        }
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int> path;
        vector<string> res;

        if (root == NULL) return res;
        traversal(root, path, res);
        return res;
    }
};

404.左叶子之和

左叶子的定义：首先必须是叶子节点（叶子节点的左右孩子为空）。同时还必须是父节点的左孩子。

本题和之前的二叉树类题目有不同之处。之前的题目遍历到哪个节点就处理哪个节点，但这题遍历到某个节点时，不能直接处理该节点，因为无法判断该节点是否其父节点的左孩子。这题的思路为遍历到某个节点，若其左孩子不为空，但左孩子的左右孩子为空，那么该节点的左孩子就是左叶子，处理该节点的左孩子即可。

本题用后序遍历比较容易，因为后序遍历是左右中，是一层层向上返回。本题也可使用迭代法。

int traversal(TreeNode* node) 
{
    // 终止条件1
    if (node == NULL) return 0;
    
    // 终止条件2，可不写，不写就会做无用的递归
    // 如果当前遍历的节点是叶子节点，那其左叶子也必定是0
    if (node->left == NULL && node->right == NULL) return 0;
    
    // 左
    int leftNum = traversal(node->left);
    // node为左叶子的父节点，左叶子为node->left
    if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) 
        leftNum = node->left->val;
    
    // 右
    int rightNum = traversal(node->right);
    // 中
    int sum = leftNum + rightNum;
    
    return sum;
}

上述代码可以精简。但不建议初学者看。

本题其实用层序遍历也可以解决，关键依然在于对于左叶子的父节点的判断，代码如下所示：

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        int res = 0;
        queue<TreeNode*> q;

        if (root == NULL) return 0;
        q.push(root);

        while (q.size())
        {
            int size = q.size();
            while (size -- )
            {
                TreeNode* node = q.front();
                q.pop();
                if (node->left && node->left->left == NULL && node->left->right == NULL) res += node->left->val;
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        return res;
    }
};

直接把queue改为stack，也可以解决本题。采用queue的写法是层序遍历，而采用stack的写法是普通迭代写法（区别于统一迭代写法）。

心得与备忘录

110.平衡二叉树

平衡二叉树：二叉树中任何一个节点左右子树的高度差不超过1。求高度要用后序遍历。
我在初次尝试中的做法较为简单，但没有进行剪枝，意味着即使某些树的子树为非平衡二叉树，依然会继续递归，而不是直接return false。这样导致程序的时间复杂度较高。
卡尔提供的解法的核心思路在于：node为根节点的二叉树是平衡二叉树则返回node的高度，是非平衡二叉树则返回-1。本解法的时间复杂度较低，原因在于当发现某个子树是非平衡二叉树时，就说明整棵二叉树都是非平衡二叉树，则一路返回-1，相当于做了剪枝的操作。
本题优先掌握递归法即可，不要求掌握迭代写法。迭代写法代码很长，且因为迭代法有很多重复的计算，导致效率很低。

257. 二叉树的所有路径

本题第一次让我接触到了回溯。更具体地说，是第一次在代码中显示地写出了回溯。
本题虽然是一个easy，但对我这个初学者来说难度不小，需要记得复习。
本题的核心思路依然是递归三部曲：
- 确定传入的参数：节点、单条路径和最终结果，后两者需要加上引用。
- 终止条件：到达叶子节点
- 单层递归逻辑：前序遍历。中节点的处理逻辑需要放在终止条件之前，否则单条路径中不包含叶子节点。左右节点的处理逻辑注意判空和回溯。
本题推荐采用我在实现中的写法，虽然代码略显复杂，但清楚地体现了回溯的过程，且不容易出错。不建议写精简的写法，容易出错，且对理解本题的原理并无帮助。

404.左叶子之和

注意本题中对于左叶子的定义。
本题不能遍历到哪个节点就处理哪个节点，而是遍历到左叶子的父节点，就处理左叶子。
本题采用后序遍历的写法，代码较为简单，结果从下往上一层层返回。本题也可采用层序遍历的套路写法。
本题有两个终止条件，第二个终止条件可以不写，但会导致多递归一层。
注意如何判断一个节点是否为左叶子的父节点：if (node->left != NULL && node->left->left == NULL && node->left->right == NULL)。
本题依然可以方便地套用层序遍历的常规代码。
我非常惊讶地发现，在本题中，若采用类似层序遍历的写法，用栈或者队列作为存放遍历过的节点的数据结构，都可以得到能够正常运行的代码。卡尔的讲义上给出的迭代法的写法并非是严格意义上的层序遍历，而仅仅是前序遍历的普通迭代写法（也并非统一迭代）。层序遍历需要用队列作为数据结构，而卡尔给的迭代写法采用了栈作为数据结构，但采用严格的层序遍历的写法依然可以解决这道题。