Day 20 Leetcode 530 501 236

链接

530.二叉搜索树的最小绝对差
501.二叉搜索树中的众数
236. 二叉树的最近公共祖先

初次尝试

530.二叉搜索树的最小绝对差

本题虽然是个easy题，但我想不出来怎么做。唯一的思路是双指针，至于怎么递归，按照怎样的顺序，我想不出来。

501.二叉搜索树中的众数

本题显然又要充分利用二叉搜索树的特性：中序遍历二叉搜索树，得到的数组是递增的，统计数组中出现频次最高的元素即可。本题我目前发现了两个需要注意的点：

1. 出现频次最高的元素可能不止一个，因此需要返回一个数组。
2. 本二叉搜索树的性质为：左子树中的所有节点小于等于根节点，右子树中的所有节点大于等于根节点。

本题似乎也应该采用双指针的做法。若pre->val和cur->val相等，则cnt数组（用于统计元素值出现的次数）中pre->val的值加1。但这里有两个问题：

• 节点的值可能为负数，因此不能将节点的值直接映射为数组的下标
• 若出现次数最多的元素不止一个，该如何返回数组

上述两个问题都不好解决，我直接看卡尔的讲解吧。

236. 二叉树的最近公共祖先

本题比较难，我拿到后没有什么想法，猜测可能要用到回溯。直接看卡尔的讲解。

实现

530.二叉搜索树的最小绝对差

目标：求任意两节点间的最小绝对差。由于是二叉搜索树，用中序遍历会成为一个有序的序列，据此思路尝试解出此题。我独立写出了本题的第一种解法：

class Solution {
public:
    vector<int> vec;

    void inorder(TreeNode* root)
    {
        if (root == NULL) return;

        inorder(root->left);
        vec.push_back(root->val);
        inorder(root->right);
    }

    int getMinimumDifference(TreeNode* root) {
        inorder(root);

        int min = INT_MAX;
        for (int i = 0; i < vec.size() - 1; i ++ )
        {
            if (min > vec[i + 1] - vec[i]) min = vec[i + 1] - vec[i];
        }

        return min;
    }
};

和98.验证二叉搜索树相同，本题应该也可以用maxvalue法和双指针法。这两种方法本质上都是不用额外的数组，直接在中序遍历时计算两个相邻节点的差值，然后选取最小的差值。现在我来尝试这两种解法。这两种解法我还是想不出来，看卡尔的讲解。

接下来讲解如何在中序遍历时利用两个指针直接得出最小绝对差，而不用把二叉树转变为数组。难点：中序遍历二叉树时前后指针如何移动（控制）。

int res = INT_MAX;

TreeNode* pre = NULL;

// 返回二叉树的某一特性或者二叉树节点的某个数值，才需要返回值。本题的情况不需要返回值
// 确切来说，一找到就需要立刻去返回的才需要返回值。需要遍历整棵二叉树且用全局变量来记录返回结果的，函数就不需要返回值
void traversal(TreeNode* cur)
{
    // 终止条件
    if (cur == NULL) return;
    
    // 单层递归逻辑：中序遍历
    traversal(cur->left); // 左
    // 中
    if (pre != NULL) res = min(res, cur->val - pre->val);
    pre = cur;
    traversal(cur->right); // 右
}

移动pre和cur的核心在于：cur由中序遍历来移动，pre由赋值移动。cur是当前节点，pre是当前节点的上一个节点。

根据上述核心代码，我写下了本题的完整代码：

class Solution {
public:
    int res = INT_MAX;
    TreeNode* pre = NULL;

    void traversal(TreeNode* cur)
    {
        if (cur == NULL) return;

        // 左
        traversal(cur->left);
        // 中
        if (pre != NULL && cur->val - pre->val < res)
            res = cur->val - pre->val;
        // 也可写作
        // if (pre != NULL) res = min(res, cur->val - pre->val);
        pre = cur;
        // 右
        traversal(cur->right);
    }

    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return res;
    }
};

本题也可以用迭代法，但不推荐。

501.二叉搜索树中的众数

二叉搜索树中可能有重复的元素。众数可能不止一个，因此输出众数的集合。暴力做法：对一棵普通的二叉树，遍历二叉树，用map统计每个元素出现的频次，然后将map转换为vector，对vector进行排序，然后在数组中求众数。

如何利用二叉搜索树的特性去求众数的集合？遍历顺序：中序遍历。中序遍历得到的数组中的所有元素是单调递增的。求众数的具体方法：先遍历一遍二叉树，记录下所有元素出现的最高频率。再遍历一遍二叉树，将出现频率为最高频率的元素放入结果集中。其实可以不遍历两遍二叉树，遍历一遍二叉树即可，需要用到一些代码技巧。

双指针算法的思路：用count来统计当前元素出现的次数。当pre->val == cur->val时，当前元素出现的次数加1。当pre->val != cur->val，则count归一。初始时，pre指向NULL，count指向左叶子节点，count也为一。当count == maxcount时，将当前元素放入结果集中。

这里有个问题：如果不事先遍历一遍二叉树，怎么知道maxcount一定是真正的最高频率？后面的具体代码实现中会处理这个问题。现在开始写具体的代码：

TreeNode* pre = NULL;
int count = 0; // 当前元素出现的频率
int maxcount = 0; // 整个二叉树中（已经遍历过的节点）的元素出现的最高频率
vector<int> res; // 结果集

// 遍历整个二叉树，结果放入全局变量中，因此递归函数不需要返回值
void traversal(TreeNode* cur)
{
    // 终止条件
    if (cur == NULL) return;
    
    // 单层的递归逻辑
    // 左
    traversal(cur->left);
    // 中：处理逻辑
    // 统计count
    if (pre == NULL) count = 1; // 双指针的初始位置：pre为NULL，cur指向左叶子节点
    else if (pre->val == cur->val) count += 1; // 当前元素出现的次数+1
    else count = 1; // 双指针指向的节点的值不相等，则count又回到1
    pre = cur; // pre跟随cur移动
    
    // 若当前节点的出现次数等于整个二叉树中元素出现的最大次数，则将其放入结果集中
    if (count == maxcount) res.push_back(cur->val);
    
    // 此时存在问题：maxcount不是真正的maxcount，因此需要代码去更新res数组
    // 实时更新res数组，就不需要遍历两遍二叉树了
    if (count > maxcount) 
    {
        maxcount = count; // 更新maxcount
        // maxcount都被更新了，原先的结果集中的结果全废了，清空res
        res.clear();
        res.push_back(cur->val); // 将当前节点的数值放入结果集中
    }
    
    // 右
    traversal(cur->right);
    
    return;
}

我也写出了遍历两次二叉树的代码，如下所示。需要特别注意的是，getmaxcount后需要重置pre和count。遍历两次二叉树的代码显得很冗余，因为基本相同的逻辑写了两遍。

class Solution {
public:
    TreeNode* pre = NULL;
    vector<int> res;
    int count = 0;
    int maxcount = 0;

    // 第一次遍历二叉树，得到maxcount
    void getmaxcount(TreeNode* cur)
    {
        if (cur == NULL) return;

        getmaxcount(cur->left);
        // 中节点
        if (pre == NULL) count = 1;
        else if (pre->val == cur->val) count += 1;
        else count = 1;
        pre = cur;
        if (count > maxcount) maxcount = count;

        getmaxcount(cur->right);
    }

    // 第二次遍历二叉树，得到结果集
    void traversal(TreeNode* cur)
    {
        if (cur == NULL) return;

        traversal(cur->left);

        // 中节点
        if (pre == NULL) count = 1;
        else if (pre->val == cur->val) count += 1;
        else count = 1;
        pre = cur;
        if (count == maxcount) res.push_back(cur->val);

        traversal(cur->right);
    }

    vector<int> findMode(TreeNode* root) {
        getmaxcount(root);
        pre = NULL; // getmaxcount后重置pre
        count = 0; // getmaxcount后重置count
        traversal(root);
        return res;
    }
};

本题也可以采用迭代法，基本上是迭代的模板加上递归法对中节点的处理逻辑。但本题推荐掌握递归法即可。

236. 二叉树的最近公共祖先

找两个节点p和q的最近公共祖先。条件：二叉树中所有节点的值都是不同的，二叉树中一定存在p和q。根节点是任何两个节点的公共祖先，所以求公共祖先没有意义，求最近公共祖先才有意义。简单的想法：找到节点p和节点q后，从下往上去遍历，直到找到公共的节点。但对二叉树，一般大家熟悉的是从根节点开始从上往下去遍历，实际上也无法从下往上去遍历，但处理顺序可以是从下往上的。回溯的过程就可以让我们去从下往上地处理结果。具体来说，可以判断某个节点的左子树是否出现过p，右子树是否出现过q，如果都出现了，就将该节点向上返回。看该节点的父节点，若父节点的左子树中没出现p，或者右子树中没出现q，则说明该节点是p和q的最近公共祖先。父节点继续将最近公共祖先节点的值向上返回，直到返回到根节点。

从下往上传递p和q节点的最近公共祖先的逻辑写在回溯过程中。想在回溯过程中达到从下往上处理的效果，一定要用后序遍历。后序遍历是左右中，中：处理逻辑。中的具体处理逻辑：判断某个节点的左子树是否出现过p，右子树是否出现过q。即在终止条件中，如果遇到了p或者q，就往上返回。如果一个节点的左子树的返回值不为空，则左子树中出现了p或者q；如果一个节点的右子树的返回值不为空，则右子树中出现了p或者q。如果当前中节点的左右子树的返回值都不为空，则当前的中节点就是p和q最近的公共祖先。还有一种情况。即p就是q的公共祖先。但本情况的处理逻辑和上面是相同的。

具体的代码：

// 返回最近的公共祖先
TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q)
{
    // 终止条件1
    if (root == NULL) return NULL;
    // 终止条件2：遇到节点p或者q，则将它们向上返回
    if (root == p || root == q) return root;
    
    // 单层递归的逻辑：后序遍历
    // 左：可以告诉我们左子树中是否出现过p或者q
    TreeNode* left = traversal(root->left, p, q);
    // 右：可以告诉我们右子树中是否出现过p或者q
    TreeNode* right = traversal(root->right, p, q);
    // 中
    // 左右子树中出现了p和q，则root是最近公共祖先，将root返回
    if (left != NULL && right != NULL) return root;
    // 左子树中没有p和q，右子树为最近公共祖先，则继续将right（即最近公共祖先）向上返回，可以参见下面的实例
    if (left == NULL && right != NULL) return right;
    // 左子树为最近公共祖先，右子树中没有p和q，则继续将left(即最近公共祖先)向上返回，和上面一行代码同理
    if (left != NULL && right == NULL) return left;
    // 左右子树都为空，则return NULL
    else return NULL;
}

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 7, q = 4
Output: 2
Explanation: The LCA of nodes 5 and 1 is 3.

以上面的二叉树为例，2的左子树返回7，右子树返回4，则2是最近公共祖先。5的左子树返回空，右子树返回2，2是7和4的最近公共祖先，则将2继续向上返回。

为什么上述代码将另一种情况也包含了？以上图为例，若p=7, q=2，则q就是最近的公共祖先。一旦遇到q就返回，就不继续向下遍历了。最终就将q返回到root节点，作为结果了。因此另一种情况不需要特别考虑。

本题的难点：

• 回溯的过程可以将结果逐层从下往上返回。
• 从下往上返回结果需要用到后序遍历。先进行左右子树的判断逻辑，再进行中节点的逻辑。只有左右子树的返回值不为空，才将中节点作为最近公共祖先返回。
• 可以举实例画图理解本题的回溯过程和后序遍历中节点的处理（返回）逻辑。
• 情况2的处理逻辑包含于情况1中。

心得与备忘录

530.二叉搜索树的最小绝对差

1. 遇到二叉搜索树，首先需要注意其在中序遍历后得到的数组是递增的这一特性。
2. 遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值。
3. 我之所以一开始没有写出本题的双指针解法，原因在于忘记了如何确定递归函数的返回值。对于本题，需要遍历整棵二叉树且用全局变量来记录返回结果，因此递归函数不需要返回值。
4. 本题的双指针法的思路和98.验证二叉搜索树相同，但两题的区别在于本题的递归函数没有返回值，而98题的递归函数返回值为bool类型。
5. 移动pre和cur的核心在于：cur由中序遍历来移动，pre由赋值移动。cur是当前节点，pre是当前节点的上一个节点。

501.二叉搜索树中的众数

1. 本题虽然是easy难度，但其实是比较难的。
2. 若是一般的二叉树，而非二叉搜索树，则本题的思路为：首先遍历二叉树，用map统计每个元素出现的次数。然后对map按照value进行排序，将排序后的map的(key, value)中最大的一个（或几个）value对应的key放入结果集中。原理不复杂，但代码实现起来比较麻烦。
3. 本题是二叉搜索树，因此想要充分利用了其性质的话，肯定要采用中序遍历。本题的核心思路依然是双指针算法。需要一个count来存储当前节点出现的次数，一个maxcount来存储整棵二叉树中出现次数最多的节点出现的次数。如果采用两次遍历的做法，那么需要先遍历一遍二叉树得到maxcount，然后再遍历一遍二叉树，将count == maxcount的节点的值存入结果集中。但实际上，遍历一遍二叉树即可完成上述操作。
4. 遍历一遍二叉树的做法：初始时，count = 1；pre->val == cur->val时，count += 1；否则，count = 1。若count == maxcount，则将当前节点的值放入结果集中。此时出现问题：maxcount不一定是整棵二叉树出现次数最多的节点出现的次数。可以用一个简单的办法解决这个问题：若count > maxcount，则更新maxcount，清空结果集，然后再往结果集中插入当前节点的值。通过这样的操作，就可以动态地去更新结果集，从而避免了对二叉树的两次遍历。

236. 二叉树的最近公共祖先

1. 本题需要自下往上处理节点，自然而然想到用回溯的思想。

2. 后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。因此本题采用后序遍历。

3. 理解以下的示意图就理解了本题：
   

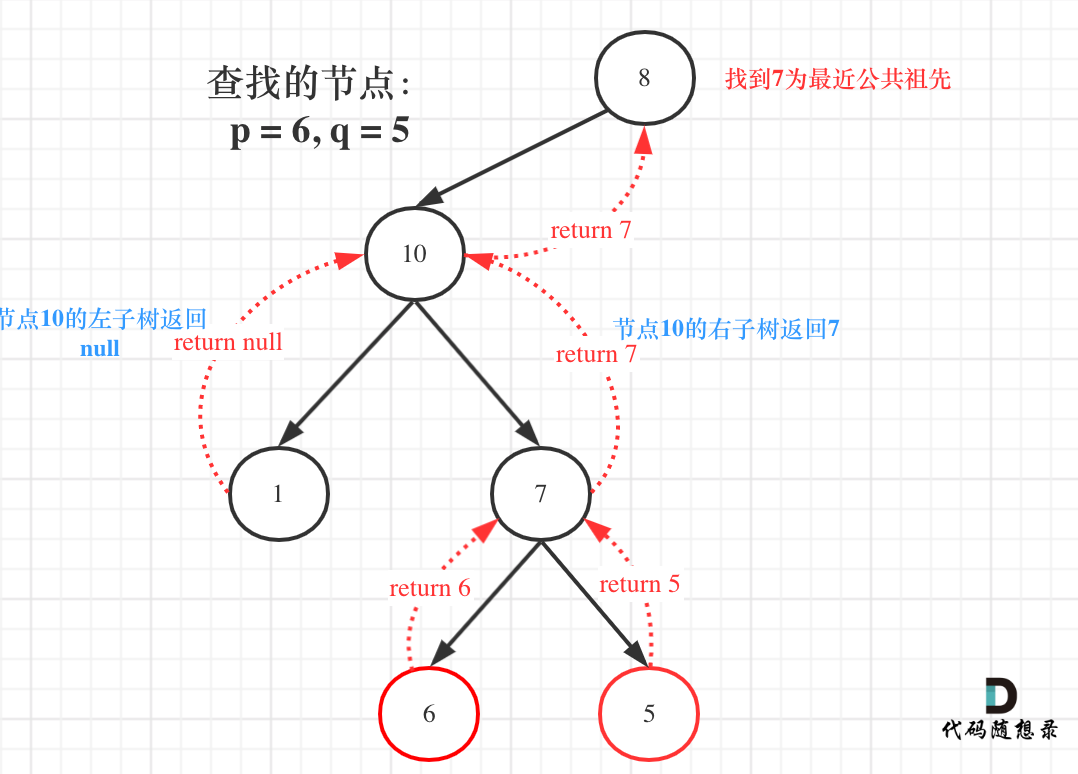
4. 本题的代码实际上非常简单而清晰，可以根据代码来理解上面的图片，本题的核心代码为中节点的处理逻辑：

   // 终止条件1
   if (root == NULL) return NULL;
   // 终止条件2：遇到节点p或者q，则将它们向上返回，对应于节点6和5将它们自身向节点7返回的过程
   if (root == p || root == q) return root;
   
   // 单层递归的逻辑：后序遍历
   // 左：可以告诉我们左子树中是否出现过p或者q
   TreeNode* left = traversal(root->left, p, q);
   // 右：可以告诉我们右子树中是否出现过p或者q
   TreeNode* right = traversal(root->right, p, q);
   // 中
   // 左右子树中出现了p和q，则root是最近公共祖先，将root返回，对应于节点7将其自身向节点10返回的过程
   if (left != NULL && right != NULL) return root;
   // 左子树中没有p和q，右子树为最近公共祖先，则继续将right（即最近公共祖先）向上返回
   // 对应于节点10将节点7向节点8返回的过程
   if (left == NULL && right != NULL) return right;
   // 左子树为最近公共祖先，右子树中没有p和q，则继续将left(即最近公共祖先)向上返回，和上面一行代码同理
   if (left != NULL && right == NULL) return left;
   // 左右子树都为空，则return NULL
   else return NULL;

   用文字来描述，本题的关键代码实现了以下功能：

   • 遇到节点p或q，就将其向上返回
   • 某个节点的左右子树中包含p和q，则该节点就是p和q的最近公共祖先，将该节点向上返回
   • 某个节点的左右子节点中的一个的返回值不为空，则说明那个返回值不为空的左/右节点为p和q的最近公共祖先，将该节点进一步向上返回
   • 其他情况下均返回空即可

5. 还有一种情况，即p是q的父节点，此时遍历到p的父节点时，p的父节点就会向上返回p，而不会继续遍历p和其下面的子树。因此本情况也包含在上述代码的逻辑中。