链接
知识
理论基础
什么是回溯法
回溯算法比较抽象,因此较难。
回溯和递归是相辅相成的,有递归就会有回溯。回溯的逻辑一般隐藏在递归函数的下面。二叉树在递归的过程中会有回溯的操作,只不过有的题目显式地用到了回溯,有的题目没有显式地用回溯。回溯函数一般指递归函数,因为没有一个函数可以完全用来回溯。
回溯法的效率:回溯法是纯暴力的搜索,并不是一个高效的算法。如果想让回溯法高效一些,可以加一些剪枝的操作。部分题能够用暴搜做出来就不错了,用层层嵌套的for循环都根本搜不出来,要依靠回溯法才能把所有结果搜出来。
使用原因以及解决的问题
回溯法能解决的问题:
- 组合问题。比如给定集合1234,找出长度为2的组合。
- 排列问题。排列强调元素的顺序,而组合不强调元素的顺序。比如集合12,求其组合,只有12一种组合;但若求其排列,有12/21两种排列。
- 子集问题。比如给定集合1234,问该集合有多少子集。
- 切割问题。比如给一个字符串,问有几种切割方式。或者加一些特定的条件,比如给一个字符串,如何切割才能保证它的子串都是回文子串,问有几种切割方式。
- 棋盘问题。比如N皇后、解数独。
如何理解回溯法
回溯法特别抽象。想要清晰地了解回溯法,最好将其抽象为一个图形结构。所有的回溯法都可以抽象为一个树形结构,确切的说是N叉树。原因:回溯就是递归的过程,递归有终止。N叉树的宽度是在回溯法中处理的集合的大小,一般用for循环遍历。树的深度是递归的深度,因为递归必有终止,递归会层层向上返回。后序讲解具体问题时,都会将具体问题抽象为对应的树形结构,方便大家理解。
回溯模板
一般来说,回溯法的递归函数都是没有返回值的,即void。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23// backtracking为习惯的起名
// 回溯法的参数一般较多,一开始时一般无法确定所有参数,写具体逻辑时遇到想用的参数,再添加参数即可
void backtracking(参数)
{
// 终止条件。到终止条件时,一般来说就可以收集结果了
// 除去子集问题和部分棋盘问题,我们一般在叶子节点收集结果
// 对于子集问题,则需要在每个节点处收集结果
if (终止条件)
{
(叶子节点处)收集结果 // 例如将子集12从数组中放入结果集中
return;
}
// 单层搜索的逻辑
// for循环用于遍历本层集合中的每个元素,对应一个节点的所有子节点
for (集合元素)
{
处理节点 // 例如将子集12放进数组中
递归函数 // 树形结构往深处走
回溯操作 // 撤销对节点的处理,例如从子集12中弹出2,再加入3,才能得到新的子集13。同理,还需要撤销3加入4,得到14的组合。没有回溯操作,就会一直加入新的元素,就不会求出所有的组合情况。
}
return;
}
每道回溯法的题目都有各自的特点,但最终的代码都离不开上述模板的风格。
总结
后序会用本期视频讲解的理论知识求解具体问题,就可以加深对本期视频讲解的理论知识的理解。
初次尝试
77. 组合
根据回溯模板,我写下了以下的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
vector<vector<int>> res; // 结果集
vector<int> tmp; // 暂时存储数据
void backtracking(int n, int k)
{
// 终止条件
if ()
{
res.push_back(tmp);
return;
}
// 单层递归逻辑
for (int i = 0; i < n; i ++ )
{
// 处理节点
tmp.push_back(i);
k -- ;
// 递归函数
backtracking(n, k);
// 回溯操作
k ++ ;
}
return;
}
vector<vector<int>> combine(int n, int k)
{
backtracking(n, k);
return res;
}
};
尽管和最终版本的代码已经非常接近,但是我不知道怎么写终止条件,也无法确定传入的参数是否齐全。先来看卡尔的讲解。
实现
77. 组合
组合中的元素是无序的。给定集合1234,找出所有大小为2的组合。有12,13,14;23,24;34。暴力做法:两层for循环。1
2
3for (int i = 0; i < size; i ++ )
for (int j = i + 1; j < size; j ++ )
cout << i << ' ' << j << endl;
两层for循环即可求解k=2下的所有组合。三层for循环即可求解k=3下的所有组合。若k很大,则要嵌套很多层for循环。因此直接用for循环是无法解决本题的,就需要用到回溯算法。
回溯算法也是一个纯暴力的方式,模拟的也是嵌套for循环的过程。回溯算法是利用递归来控制有多少层for循环。递归里的每一层都是一个for循环。嵌套n层for循环即相当于递归n层。
所有的回溯法都可以抽象为一个树形结构。以本题为例,画回溯算法搜索的过程。
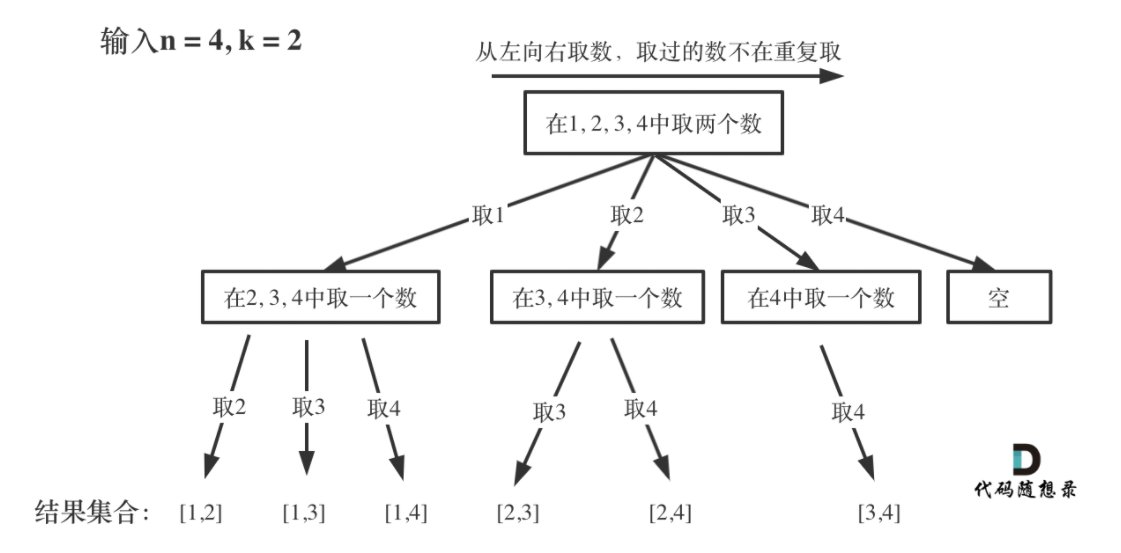
上述树形结构的叶子节点就是要求的所有组合。第一次取数是从集合中依次取,第二次取数是取第一次取的数的后面一个数,这样才能保证不重不漏。通过传入参数startIndex来实现这点,即控制每次搜索的起始位置。
二叉树的题目有递归三部曲,回溯算法也有回溯三部曲(回溯函数即递归函数,二者不作区分):
- 递归函数的参数和返回值,返回值一般为void
- 确定递归的终止条件
- 单层搜索(递归)的逻辑
根据回溯三部曲对着上述图示写组合问题的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31// 一个组合存放在一个一维数组中,名为path
// 还需要一个二维数组res,将所有集合放在一起,作为结果集返回
// 上述两个数组可以作为加引用的参数,也可以作为全局变量。但参数不宜过多,会影响代码的可读性,因此将它们放入全局变量中
vector<int> path;
vector<vector<int>> res;
// n是集合中数的个数,k是组合的大小
// startIndex的作用:本层递归结束后,下一层递归如何知道从哪个数开始取,就要用到startIndex
// startIndex是本层递归搜索的起始位置,初始时为1,即从1开始搜索
void backtracking(int n, int k, int startIndex)
{
// 终止条件,到叶子节点时,收集结果并返回
// path的大小为k,说明找到了大小为k的组合,将之放入结果集并返回
if (path.size() == k)
{
res.push_back(path); // 收集结果
return;
}
// 单层搜索的逻辑
// 每层都是一个for循环,起始点从startIndex开始
for (int i = startIndex, i <= n; i ++ )
{
// 处理节点
path.push_back(i);
// 递归过程, i + 1才能让下一层递归从下一个节点开始搜索
backtracking(n, k, i + 1);
// 回溯过程。不可以一直往里加,得到一个结果后需要弹出旧的元素
path.pop_back();
}
}
时间复杂度:$O(n \times 2^n)$
空间复杂度:$O(n)$
原因:
对时间复杂度
解空间的大小
对于组合问题,如生成一个集合的所有子集,解空间包含了该集合的所有可能子集。对于包含$n$个元素的集合,其子集总数是$2^n$。这是因为每个元素在每个子集中都有出现或不出现两种可能,因此,子集的总数是$2^n$。
每个解的生成时间
虽然生成每个子集看起来很快,但是实际上,为了构建每个子集,可能需要遍历所有元素来决定每个元素是否包含在当前子集中,这需要$O(n)$的时间。因此,对于所有子集,生成时间是每个子集的生成时间与子集总数的乘积,即$O(n \times 2^n)$。
对空间复杂度
在讨论空间复杂度时,我们通常关注的是算法在执行过程中需要额外分配的空间量。对于回溯算法来说,主要的空间消耗源于两部分:递归调用的栈空间和用于存储当前解的路径(在此例中为 path)。以下是详细分析:递归栈空间
在回溯算法中,递归的深度决定了栈空间的使用量。在这个特定的问题中(从 n 中选择 k 个数的组合),递归的最大深度是 k,因为每一层递归对应于选择一个元素,直到选择了 k 个元素。因此,递归栈的空间复杂度是 O(k)。存储当前解的路径空间
path 变量用于存储当前的部分解,即已选择的元素集合。因为一次最多选择 k 个元素,所以 path 的最大长度也是 k。因此,存储 path 所需的空间也是 O(k)。结果集 result
虽然result用来存储所有可能的组合,其大小可以达到组合数$C(n, k)$,但在分析空间复杂度时,我们通常不把输出空间计算在内,因为这部分空间是用来存储算法的最终结果,而非算法执行过程中的临时数据。如果包括result的空间,空间复杂度确实是$O(C(n, k))$,但这不是额外的空间,而是算法结果的必要空间。
本题的完整代码如下所示:
1 | class Solution { |
本题的代码并不复杂,基本是按照回溯法的模板来的。本题还可以做剪枝。回溯法是一个纯暴力的算法,想优化就要做剪枝。接着详细讲如何做剪枝,以及回溯算法常见的剪枝套路。
组合问题的剪枝操作
回溯算法是一种纯暴力的算法,优化就是做剪枝,但也改变不了其暴力算法的本质。如何做剪枝操作?
以n=4, k = 4为例。
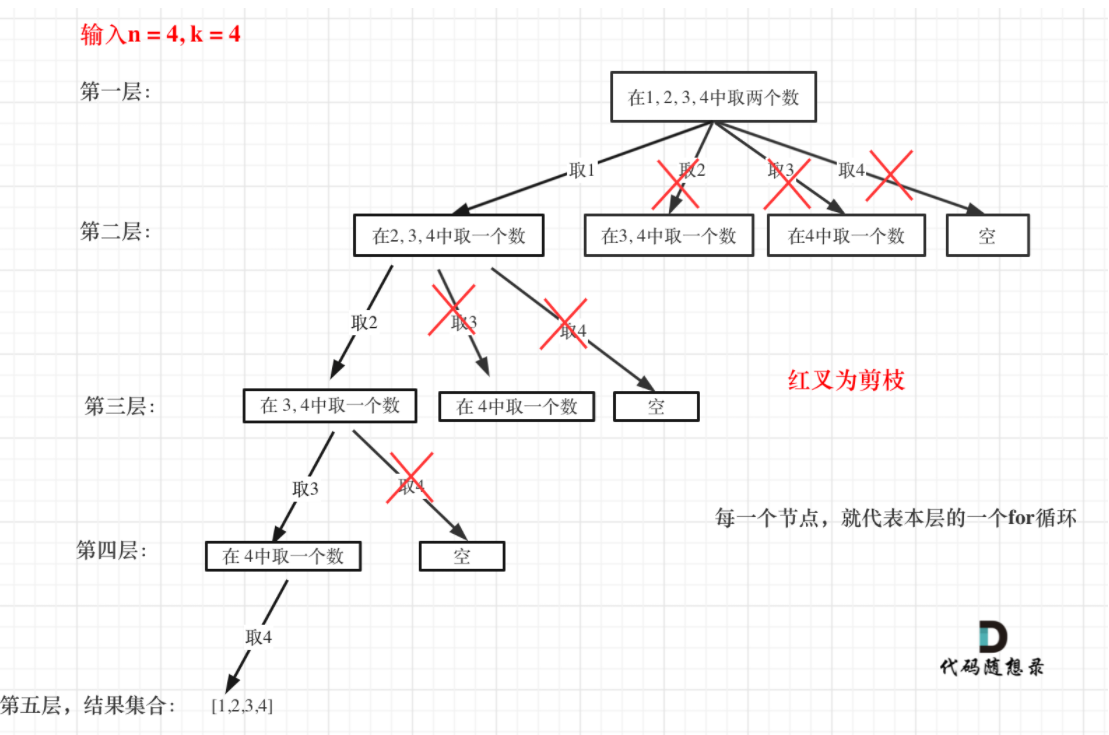
对取2,取3和取4的分支,可以做剪枝。若不做剪枝,回溯算法会搜索整个树形结构,因此剪枝的效果非常明显。剪枝的代码该怎么写?
1 | // 剪枝操作在单层搜索逻辑中 |
现在的具体问题是:如何缩小i的范围?
总共要选取k个元素,当前选取了path.size()个元素,还剩下k - path.size()个元素有待选取。因此i至多从n - (k - path.size()) + 1开始。加1的原因是起始位置包括了startIndex。也可以举具体的例子。以n=4, k=3, path.size()=0为例,i至多从2开始枚举(这意味着i可以从1开始枚举,也可以从2开始枚举,但若从3开始枚举,则必然搜索不到大小为3的组合)。因此对上述代码修改为:
1 | for (int i = startIndex; i <= n - (k - path.size()) + 1; i ++ ) |
这样可以确保在搜索的范围中可以找到大小为k的组合。剪枝的操作改动本处即可,代码其他地方不需要做改动。
上述剪枝操作在回溯算法的剪枝操作中特别常见。大部分回溯算法的剪枝操作都是在i的范围里做文章,即缩小i的范围。
心得与备忘录
77. 组合
- 本题的一个直接的想法是用k层for循环暴力解决,然而由于k的大小不确定,有待输入,因此需要用回溯法。回溯算法也是一个纯暴力的方式,模拟的也是嵌套for循环的过程。回溯算法是利用递归来控制有多少层for循环。递归里的每一层都是一个for循环。嵌套n层for循环即相当于递归n层。
- 所有回溯法的题目都可以抽象为一个树形结构,本题的树形结构参加实现部分。
- 基于本题的树形示意图,以及回溯法的模板代码,就可以写出本题的具体代码。需要特别注意的是,本题的递归函数需要传入三个参数,除去n和k外,还需要传入
startIndex。这是因为每层递归的起始点都需要在上一层递归起始点的基础上加1,因此需要一个参数来标明当前这层递归的起始点。 - 本题可以进行剪枝优化。
组合问题的剪枝操作
可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了,那么就没有必要搜索了。
注意代码中i,就是for循环里选择的起始位置。
1
for (int i = startIndex; i <= n; i++)
接下来看一下优化过程如下(可以画线段图理解):
- 已经选择的元素个数:
path.size(); - 还需要的元素个数为:
k - path.size(); - 在集合n中至多要从该起始位置:
n - (k - path.size()) + 1,开始遍历。若i超过了这个最大的起始位置,则组合中凑不齐k个元素
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,
n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。从2开始搜索都是合理的,可以是组合[2, 3, 4]。- 已经选择的元素个数:
上述剪枝操作在回溯算法的剪枝操作中特别常见。大部分回溯算法的剪枝操作都是在i的范围里做文章,即缩小i的范围。