YifanChen's Blog

一个专注技术的新手程序员

0%

Day 25 Leetcode 216, 17

发表于 更新于 分类于

链接

216.组合总和III
17.电话号码的字母组合

初次尝试

216.组合总和III

针对本题，我沿用上题77. 组合的代码，只是在终止条件中添加了条件：sum(path) == n，并在单层搜索逻辑中将终止条件改为i = 9，即可解决本题。据此，我独立写出了本题的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    int sum(vector<int> path)
    {
        int s = 0;
        for (int i = 0; i < path.size(); i ++ )
            s += path[i];
        return s;
    }

    void backtracking(int k, int n, int startIndex)
    {
        // 终止条件
        if (path.size() == k && sum(path) == n)
        {
            res.push_back(path);
            return;
        }

        // 单层搜索逻辑
        for (int i = startIndex; i <= 9; i ++ )
        {
            // 处理节点
            path.push_back(i);
            // 递归
            backtracking(k, n, i + 1);
            // 回溯
            path.pop_back();
        }
        return;
    }

    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(k, n, 1);
        return res;
    }
};

本题应该也是可以进行剪枝优化的。首先的要求当然还是k个数，因此i最大只能取到9 - k + path.size() + 1，即10 - k + path.size()。但这样会导致TLE（超时），原因尚不清楚。直接看卡尔的讲解。

17.电话号码的字母组合

本题应该还是属于组合问题的范畴。先尝试画出本题的树形结构。相当于每个数字对应三个字母，第一个数字对应的三个字母和第二个数组对应的三个字母间进行组合。若有n个数字，则有3n个字母，放入一个string a中，第一个字母从a[0]-a[2]中取，第二个字母从a[3]-a[5]中取，以此类推。相当于依然是一个组合问题，只不过每一层递归for循环的开始和结束是不固定的，需要用上述规则进行更新。据此，我尝试独立写出本题的代码框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
public:
    vector<string> res;
    string path;
    string all;

    // 将digits按照数字和字母间的对应关系转换为all字符串
    void transfer(string digits)
    {
        for (char c: digits)
        {
            if (c == '2') all += "abc";
            else if (c == '3') all += "def";
            else if (c == '4') all += "ghi";
            else if (c == '5') all += "jkl";
            else if (c == '6') all += "mno";
            else if (c == '7') all += "pqrs";
            else if (c == '8') all += "tuv";
            else all += "wxyz";
        }
    }

    void backtracking(string digits, int startIndex, int endIndex)
    {
        // 终止条件
        if (path.size() == digits.size()) res.push_back(path);

        // 单层递归逻辑
        for (int i = startIndex; i <= endIndex; i ++ )
        {
            // 处理节点
            path += all.substr(startIndex, endIndex);
            // 递归
            backtracking(digits, startIndex, endIndex);
            // 回溯
            path -= all.substr(startIndex, endIndex);
        }
    }

    vector<string> letterCombinations(string digits) {
        
    }
};

遇到的难点：startIndex和endIndex不好确定，因为部分数字不止对应三个字母。直接看卡尔的讲解。果然涉及字符串的题目都不好做啊。

实现

216.组合总和III

[1, 9]。和为n，个数为k的所有组合。本题和上题77. 组合的区别：限制和为n，集合是固定的（1-9），因此相当于在77. 组合的基础上加了一个和的限制。组合不强调元素间的顺序，排列强调元素间的顺序。暴力做法，当k=2时，两层for循环遍历1-9，找到两个相加等于n的数。暴力的想法代码没法写，所有要用回溯算法。回溯算法也是暴力的方式，只不过回溯算法通过递归的方式帮助我们控制for循环的嵌套层数，递归n层即相当于模拟了n层嵌套的for循环。

本题的树形结构如下所示：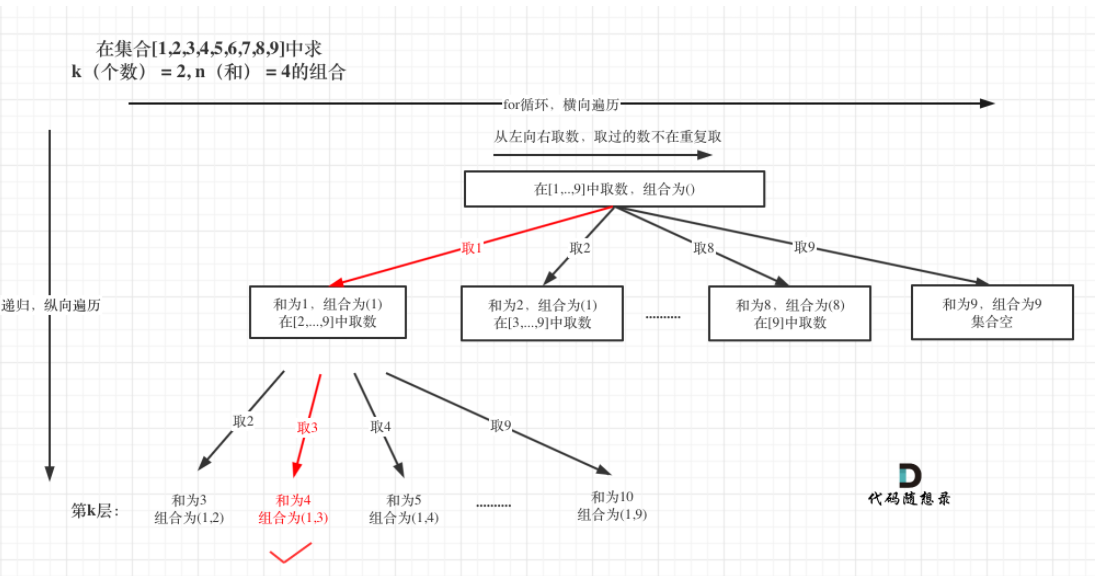
Snipaste_2024-05-02_03-55-06.png

树的深度为k，树的宽度是当前层的集合中的元素的个数。现在来写具体的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
vector<int> path;
vector<vector<int>> res;
int sum;

// sum为当前路径已有的和, 将其与targetSum(即n)做一个比较，相等即符合题目的要求
// 本题的startIndex用途同77. 组合中的startIndex，初始值为1
void backtracking(int targetSum, int k, int sum, int startIndex)
{
    // 终止条件
    if (path.size() == k)
        if (targetSum == sum)
            res.push_back(path);
    
    // 单层搜索的逻辑
    for (int i = startIndex; i <= 9; i ++ )
    {
        // 处理节点
        sum += i;
        path.push_back(i);
        // 递归
        backtracking(targetSum, k, sum, i + 1);
        // 回溯
        sum -= i;
        path.pop_back();
    }
}

完整的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(int k, int n, int startIndex, int sum)
    {
        // 终止条件
        if (path.size() == k && sum == n)
            res.push_back(path);
        
        // 单层搜索逻辑
        for (int i = startIndex; i <= 9; i ++ )
        {
            // 处理节点
            sum += i;
            path.push_back(i);
            // 递归
            backtracking(k, n, i + 1, sum);
            // 回溯
            sum -= i;
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(k, n, 1, 0);
        return res;
    }
};

接下来对上述代码进行剪枝优化。第一个剪枝在于满足targetSum的要求。剪枝代码放在终止条件之前：

1
2
if (sum > targetSum)
    return;

还有一个剪枝（满足集合中元素个数的要求），和77.组合中的剪枝是相同的。当前组合中有path.size()个元素，还需要k - path.size()个元素，因此i的最大起始位置为9 - (k - path.size()) + 1。因此：

1
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i ++ )

加上完整的剪枝优化后的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(int k, int n, int startIndex, int sum)
    {
        // 剪枝操作1
        if (sum > n) return;

        // 终止条件
        if (path.size() == k && sum == n)
            res.push_back(path);
        
        // 单层搜索逻辑
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i ++ ) // 剪枝操作2
        {
            // 处理节点
            sum += i;
            // if (sum > n) return;也可以放在此处
            path.push_back(i);
            // 递归
            backtracking(k, n, i + 1, sum);
            // 回溯
            sum -= i;
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(k, n, 1, 0);
        return res;
    }
};

我发现，若仅仅进行剪枝操作2，但不进行剪枝操作1，程序就会报错：TLE。

我还发现，尽管if (sum > n) return;放在sum += i之后，程序可以通过测评。但正统的写法应当为在剪枝前，先把回溯给做了，否则可能会漏掉满足要求的组合（程序没有进行回溯，就试图去寻找新的满足要求的组合了）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 当然这个剪枝也可以放在调用递归之前，只不过要记得把回溯操作给做了
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { 
    // 处理节点
    sum += i; 
    path.push_back(i); 
    if (sum > targetSum) { // 剪枝操作
        sum -= i; // 剪枝之前先把回溯做了
        path.pop_back(); // 剪枝之前先把回溯做了
        return;
    }
    // 递归
    backtracking(targetSum, k, sum, i + 1); 
    // 回溯
    sum -= i; 
    path.pop_back(); 
}

本题的时间和空间复杂度同77.组合的时空复杂度。

17.电话号码的字母组合

电话拨号盘，每个数字代表一个字符串。首先需要做映射。将输入的字符串（一串数字）映射为对应的字符串。可以用map或者二维数组做映射，这里使用二维数组。数组中的每个元素是字符串。

1
2
3
4
5
6
7
8
9
10
11
12
string letterMap[10] = {
    " ", // 0
    " ", // 1
    abc, // 2
    def, // 3
    ghi, // 4
    jkl, // 5
    mno, // 6
    pqrs, // 7
    tuv, // 8
    wxyz, // 9
}

这样拿到digits中的数字，将其作为下标放入字符串，即可得到数字对应的字符串（举例：letterMap[2] = "abc"）。

暴力做法：输入两个数字，则要进行两重for循环。输入n个数字，则要进行n重for循环。此时想到用回溯算法进行暴力求解。回溯算法可通过递归的方式实现对for循环的嵌套。以输入2，3为例，尝试画出本题的树形结构：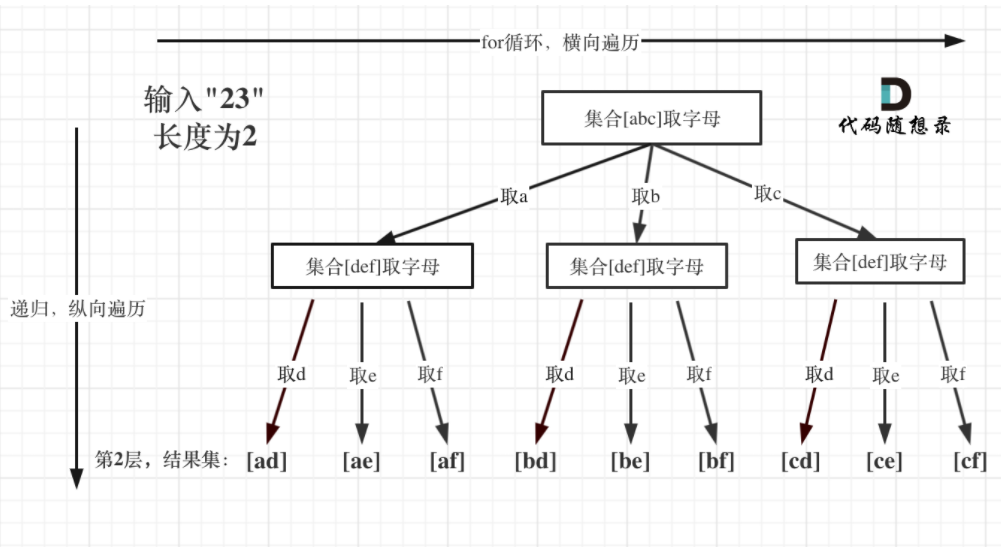
Snipaste_2024-05-02_22-19-15.png

结果就在树形结构的叶子节点中。树的深度是输入数字的个数，树的宽度由每一个数字对应的字符串的长度控制。现在尝试写本题的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
string s; // 用于存储单个结果
vector<string> res; // 收获结果集

// index用于标识传入的字符串digits在当前递归中遍历到哪一个字符（实际上是数字）了
// startIndex一般用于一个集合中求组合，避免得到重复的组合
// 本题是在多个集合中各取一个元素出来做组合，因此不需要startIndex来帮助控制集合中之前遍历过哪些元素
void backtracking(string digits, int index)
{
    // 终止条件
    // index指向digits的最后一位的下一位，才终止。若index指向digits的最后一位，其后应该还有处理最后一位的逻辑
    if (index == digits.size()) 
    {
        res.push_back(s); // 收获结果
        return;
    }
        
    // 单层搜索逻辑
    // 取出digits中的数字
    int digit = digits[index] - '0'; // 字符转换为数字
    // 找出digit对应的字符串
    string letter = letterMap[digit];
    // 遍历digit对应的字符串
    for (int i = 0; i < letter.size(); i ++ )
    {
        // 处理节点
        s.push_back(letter[i]);
        // 下一层递归，index后移一位
        backtracking(digits, index + 1);
        // 回溯
        s.pop_back();
    }
}

本题看似复杂，但画图理解后逻辑清晰，代码也不长。

可以将代码写得更简洁，递归函数传入三个参数：void backtracking(string digits, int index, string s)，然后单层搜索逻辑的三行代码写成一行：backtracking(digits, index + 1, s + letter[i]);。s的值本身并没有改变，这就是将回溯的过程隐藏在参数中了。

本题完整可运行的程序如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    string s; // 存储单个组合
    vector<string> res; // 结果集

    // 存储数字和字符串之间的映射关系
    vector<string> letterMap = {
        " ", // 0 
        " ", // 1
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz" // 9
    };

    // index用于标记当前层遍历到了digits中的哪个位置
    void backtracking(string digits, int index)
    {
        // 终止条件
        if (index == digits.size())
        {
            res.push_back(s);
            return; // 这个return不能去掉，否则程序会报错
        }
        
        // 单层递归逻辑
        int digit = digits[index] - '0'; // 取出当前层的数字
        string letter = letterMap[digit]; // 取出当前层需要遍历的字符串
        for (int i = 0; i < letter.size(); i ++ )
        {
            // 处理节点
            s.push_back(letter[i]);
            // 向下一层递归
            backtracking(digits, index + 1);
            // 回溯
            s.pop_back();
        }
        return; // 这个return可要可不要，但为了和回溯法模板保持一致，因此还是加上
    }

    vector<string> letterCombinations(string digits) {
        if (digits.empty()) return res; // 必须加上这句话，特判digits为空的情况
        backtracking(digits, 0);
        return res;
    }
};

简化后的写法（隐藏回溯逻辑）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    string s;
    vector<string> res;

    vector<string> all = {
        "",
        "",
        "abc",
        "def",
        "ghi",
        "jkl",
        "mno",
        "pqrs",
        "tuv",
        "wxyz"
    };

    void backtracking(string digits, int index, string s)
    {
        if (index == digits.size())
        {
            res.push_back(s);
            return;
        }

        // 单层搜索逻辑
        int digit = digits[index] - '0';
        string letter = all[digit];
        for (int i = 0; i < letter.size(); i ++ )
            backtracking(digits, index + 1, s + letter[i]);
    }

    vector<string> letterCombinations(string digits) {
        if (digits.empty()) return res;
        backtracking(digits, 0, s);
        return res;
    }
};

时间复杂度分析

对于每个按键，电话按键可能对应不同数量的字母：

  • 按键 2, 3, 4, 5, 6, 8 每个都对应 3 个字母。
  • 按键 7 和 9 对应 4 个字母。

如果输入的字符串中有 m 个按键对应 4 个字母，n 个按键对应 3 个字母，那么所有可能的组合数量是 4^m * 3^n。因为这是回溯算法的常见分析模式，每一步选择会进入下一层递归，直到达到输入字符串的长度。在每一层递归中，根据当前按键可能的字母数量，我们有不同的选择分支。

因此，整个算法需要考虑的总路径数或调用次数是 O(4^m * 3^n)。

空间复杂度分析

空间复杂度主要由两部分构成：

  1. 递归调用栈：最大深度为输入字符串的长度，即 m + n。然而，这通常认为是 O(m+n)，不是主要的空间消耗部分。

  2. 输出存储空间：存储所有可能组合的空间，这是算法的主要空间消耗。每个组合都是一个新的字符串，因此需要的总空间是与生成的组合数量相同，即 O(4^m * 3^n)。

如果空间复杂度中不计入输出存储空间，则空间复杂度是O(m+n)。若计入，则是O(4^m * 3^n)。

心得与备忘录

216.组合总和III

  1. 本题的思路和77.组合的完全相同，只不过加了限制条件：组合中所有元素之和为n。
  2. 本题有两种写法。第一种是我在初次尝试中的写法，最大限度地沿用了77.组合的代码，只不过另外实现了一个sum函数来统计path数组中所有元素之和，并在终止条件中与n进行比较。这种写法存在一个巨大的缺陷，就是无法进行剪枝。因为只有实现了剪枝操作1：if (sum > n) return;后，才能实现剪枝操作2：for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i ++ )，而写法1的递归函数的参数中没有sum，因此剪枝操作1必然无法实现，这导致剪枝操作2也无法实现（强行添加剪枝操作2，程序直接报错TLE（超时））。
  3. 本题的第二种写法更为正统，递归函数传入的参数中包含了sum，即当前path数组中元素之和。需要特别注意的是，处理节点的过程和回溯过程是一一对应的，sum在处理有加，在回溯就要有减。
  4. 基于本题的第二种写法，可以对代码进行两种剪枝操作。剪枝操作1：if (sum > n) return;。该操作可以放在终止条件之前，也可以放在单层搜索逻辑中处理节点时对sum的计算之后（具体细节详见实现部分，建议不要纠结这里的细节）。剪枝操作2：for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i ++ )。这和77.组合中的剪枝操作完全相同。
  5. 只有实现了剪枝操作1后，才能实现剪枝操作2。若单独实现剪枝操作2，会导致程序超时（TLE）。

17.电话号码的字母组合

  1. 本题的两大创新之处：index和letterMap。前者用于表示遍历digits遍历到了哪一位，后者用于表示数字和字符串之间的映射关系。

  2. 画出树形结构对于解决回溯法问题的帮助：确定树形结构的宽度，可以确定单层搜索逻辑中的for循环怎么写；确定树形结构的深度，可以确定单层搜索逻辑中的递归部分怎么写。

    Snipaste_2024-05-02_22-19-15.png

    在本题中，树的当前层中的各个节点是letters中的各个元素：

    1
    2
    int digit = digits[index] - '0';
    string letters = letterMap[digit];

    树的深度是digits.size()，可通过index + 1不断向树的下一层递归。

  3. 如果输入的字符串中有 m 个按键对应 4 个字母，n 个按键对应 3 个字母，则本题的时间复杂度和空间复杂度都是$O(4^m \times 3^n)$。

  4. 本题看题意较为麻烦，但如果能画出树形结构，同时学会使用vector<string>来存储数字和字符串之间的映射关系，然后通过index来取出特定数字对应的字符串，就可以写出简明而清晰的代码。

  5. 写本题代码时，最好参照回溯法的模板代码，不要省略return，否则可能导致报错。另外，在主函数中要特判digits为空的情况。