Day 26 Leetcode 39, 40, 131

链接

39.组合总和
40.组合总和II
131.分割回文串

知识

40.组合总和II

创建一个和a数组大小相同的b数组，将其中的元素全部置为0。

vector<int> a;
vector<int> b(a.size(), 0);

131.分割回文串

substr(i, j) 会从索引 i 开始，取长度为 j 的子字符串。

void backtracking(const string& s, int startIndex)中使用const的原因：

1. 防止修改：const 关键字确保 s 字符串在 backtracking 函数中不会被修改。这是一种安全措施，可以防止函数意外地更改输入数据，从而保持数据的完整性。在处理函数参数时，尤其是在不应该或不需要修改输入的情况下，使用 const 可以提供这种保护。
2. 接口设计：在函数原型中使用 const 声明参数可以向函数的用户清楚地表明这个参数是用来输入数据的，不应该被函数改变。这有助于提高代码的可读性和可维护性，使得其他开发者更容易理解每个函数的作用和行为。

初次尝试

39.组合总和

本题是集合里元素可以用无数次，那么和组合问题的差别，其实仅在于startIndex上的控制。本题若是想不重不漏，则下一层遍历的起始位置应该与上一层取出的数相同。而对于组合问题，下一层遍历的起始位置应该是上一层取出的数的下一个（因为组合问题中的元素不能重复使用）。据此，我写出了以下的代码。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& candidates, int target, int s, int startIndex)
    {
        if (s > target) return;

        // 终止条件
        if (s == target)
        {
            res.push_back(path);
            return;
        }

        // 单层搜索逻辑
        for (int i = startIndex; i < candidates.size(); i ++ )
        {
            // 处理节点
            s += candidates[i];
            path.push_back(candidates[i]);
            // 递归
            backtracking(candidates, target, s, i);
            // 回溯
            s -= candidates[i];
            path.pop_back();
        }
        return;
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return res;
    }
};

40.组合总和II

本题我能顺畅地写出不加去重的版本，如下所示。但对去重没有思路。

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& candidates, int target, int s, int startIndex)
    {
        // 终止条件
        if (s > target) return;

        if (s == target) 
        {
            res.push_back(path);
            return;
        }

        // 单层搜索逻辑
        for (int i = startIndex; i < candidates.size(); i ++ )
        {
            // 处理节点
            path.push_back(candidates[i]);
            s += candidates[i];
            // 递归
            backtracking(candidates, target, s, i + 1);
            // 回溯
            path.pop_back();
            s -= candidates[i];
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return res;
    }
};

对以下测试样例会出现报错：

candidates =
[10,1,2,7,6,1,5]
target =
8
Output
[[1,2,5],[1,7],[1,6,1],[2,6],[2,1,5],[7,1]]
Expected
[[1,1,6],[1,2,5],[1,7],[2,6]]

很明显，上述代码是需要去重的。

131.分割回文串

拿到本题，我没有思路，因为没有做过分割问题，直接看卡尔的讲解。

实现

39.组合总和

本题与组合问题的区别：集合中的元素可以重复选取，组合中元素的数量不加限定。集合中都是正整数（若有0，则会进入死循环），且集合中没有重复的元素（这意味着不用做去重的操作）。

本题通过和来限制树的深度，而组合问题通过组合中元素的数量来限制树的深度。本题的树形结构如下所示：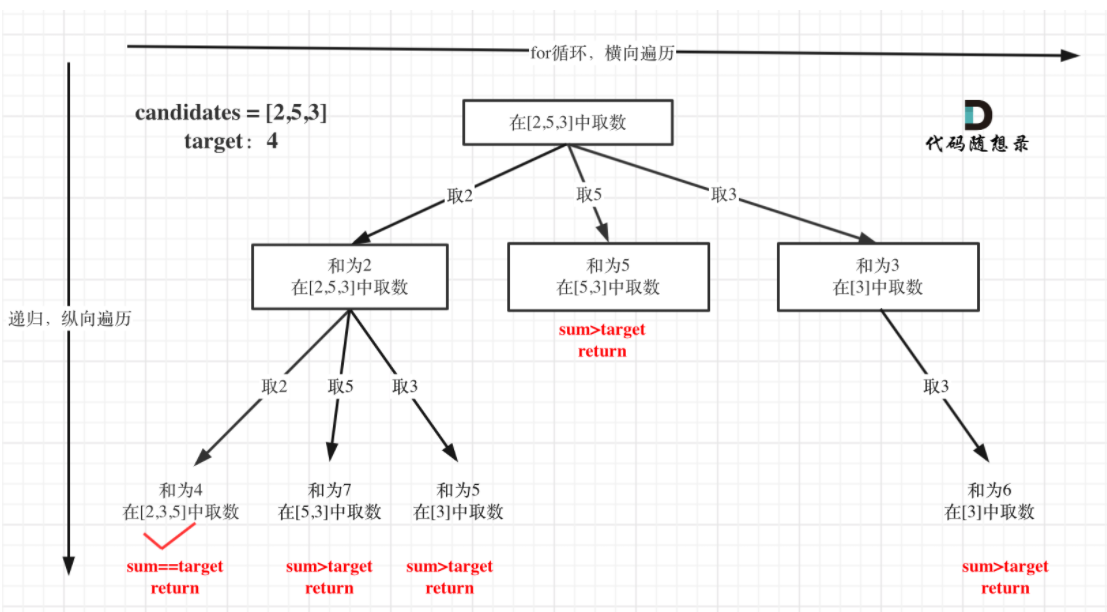

由于集合中的元素可以重复使用，因此下一层的集合中应该包括本层选取的元素。现在开始写本题的代码：

vector<vector<int>> res;
vector<int> path;

// 可以用sum表示组合的和，也可以不用sum，让target不断做减法，直到target == 0
// startIndex用于设置下一层递归的起点
void backtracking(vector<int>& candidate, int target, int sum, int startIndex)
{
    // 终止条件
    if (sum > target) return;
    if (sum == target)
    {
        res.push_back(path);
        return;
    }
    
    // 单层搜索的逻辑
    for (int i = startIndex; i < candidate.size(); i ++ )
    {
        // 处理节点
        path.push_back(candidate[i]);
        sum += candidate[i];
        // 递归，注意下一层的startIndex是从i开始，因为集合中的元素可以重复选取
        backtracking(candidate, target, sum, i);
        // 回溯
        sum -= candidate[i];
        path.pop_back();
    }
}

上述代码和回溯算法的模板是类似的。本题依然可以做剪枝的操作。具体来说，是对for循环进行剪枝。对candidate数组进行排序后，若某个分支的和大于target，那么就没必要对其后面的分支进行搜索了。加入剪枝操作的完整代码如下所示（注意添加了注释的部分，就是实现剪枝的具体代码）：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& candidates, int target, int s, int startIndex)
    {
        if (s > target) return;
        if (s == target)
        {
            res.push_back(path);
            return;
        }

        // 剪枝操作
        for (int i = startIndex; i < candidates.size() && s + candidates[i] <= target; i ++ )
        {
            s += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, s, i);
            s -= candidates[i];
            path.pop_back();
        }
        return;
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end()); // 排序
        backtracking(candidates, target, 0, 0);
        return res;
    }
};

剪枝操作总结：对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]，相当于把下一层组合可能的sum从小到大扫了过去）已经大于target，就可以结束本轮for循环的遍历。

• 时间复杂度: $O(n \times 2^n)$，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此。本题的时间复杂度分析同77. 组合。

• 空间复杂度: $O(target)$

为何是$O(target)$:

1. 递归栈深度： 空间复杂度首先取决于递归调用的最大深度，因为这直接影响了调用栈的大小。在组合总和问题中，你可以多次选择同一个数字，直到其和超过目标值 target 或恰好等于 target。最糟糕的情况发生在选择了最小元素直到达到 target 时，这种情况下，递归的最大深度大约是 target / min(candidates)。如果最小的候选数很小，理论上递归的深度可以接近 target。
2. 路径存储： 在递归过程中，我们还需要存储当前的组合路径（即当前选取的数字集合）。在最坏的情况下，即当所有选取的数字加起来等于 target 时，路径的长度也可以接近于 target / min(candidates)。尽管路径的具体长度依赖于候选数字的大小，但在分析空间复杂度时，我们考虑最坏情况，即多次选取最小值，使得路径长度和递归深度都接近于 target。

40.组合总和II

本题差别：本题的集合中有重复的元素（之前的所有组合问题的集合中都没重复元素），不能有重复的组合。这说明我们要去重。另外，集合中的元素在组合中只能使用一次，这需要用一个变量进行控制。

一种朴素的想法：用之前的方法搜索组合，搜索出若干组合，其中肯定有重复的。用map或者set进行去重，输出去重后的所有组合。本方法实现起来较麻烦，且特别容易超时。

接下来介绍在搜索的过程中直接去重的方法：使用过的元素不重复使用。为了讲清楚本题的去重过程，卡尔自创了两个词汇：树层去重，树枝去重。去重要考虑到这两个维度。接下来画树形图，从两个维度看如何去重。去重前还需要对集合进行排序。去重需要一个数组used来告诉我们哪些元素使用过，哪些元素没用过。用过的元素的下标在used中对应的值为1，没用过的元素的下标在used中对应的值为0。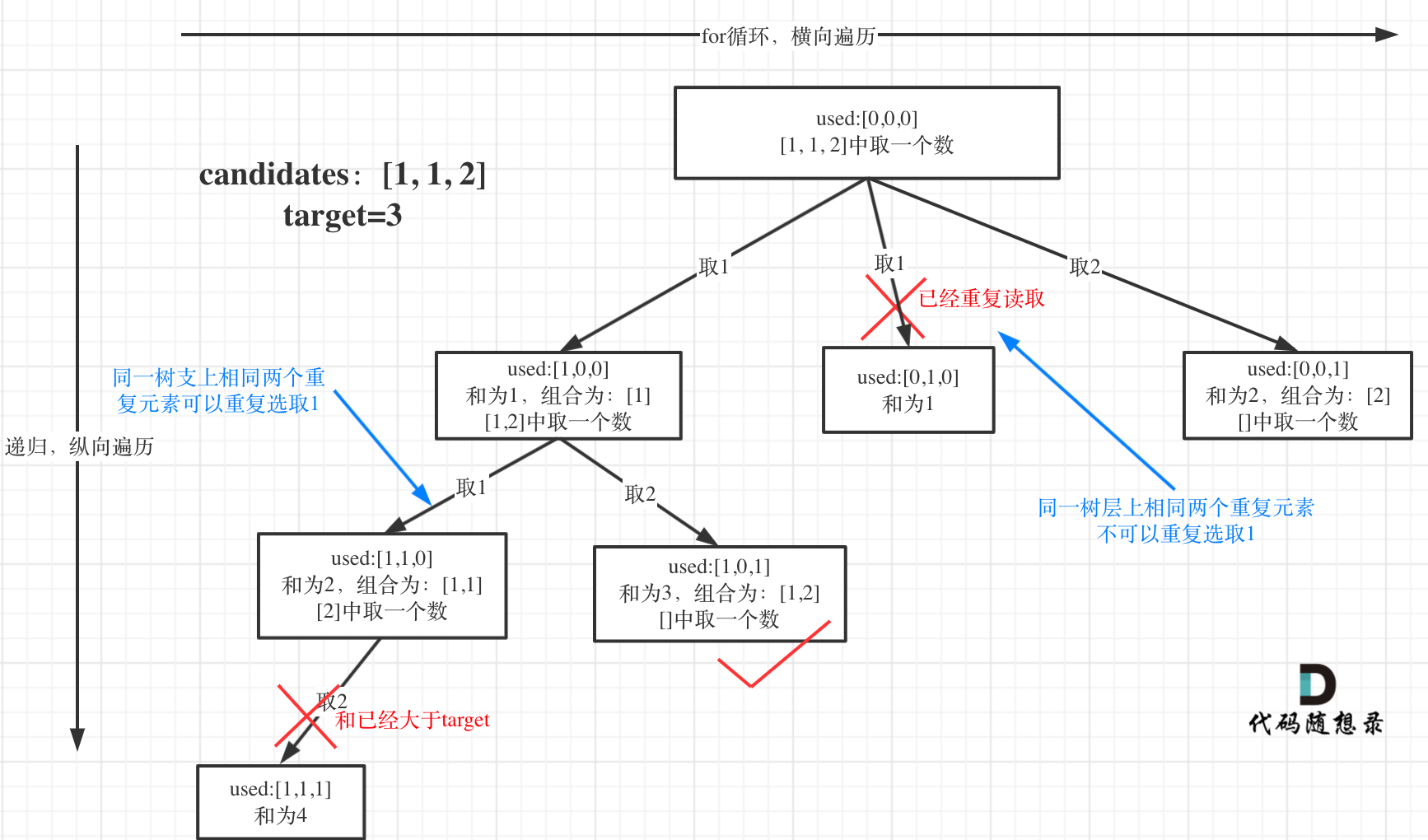

上述树除去used数组外的基本部分，还是下一层第一个取的数是上一层取的数往后挪一位（即backtracking(candidates, target, s, i + 1)）。这样的目的是避免重复。对于树枝（树往深度方向走），是可以重复取值的，因为取的是一个集合中不同位置的数值相同的元素。对于树层（同一层树往横向走），不可以重复取值，必然会与之前的某个组合重复。对集合排序的目的就是将值相邻的元素放在一起，若同一层的两个分支的值相同，那么靠左边的分支会包含靠右边的分支的所有情况。因此去重的关键在于树层去重。具体的代码如下所示：

vector<int> path;
vector<vector<int>> res;

// 本代码的重点在于树层去重的过程
// used数组用于标记某个元素是否使用过，用过1，没用过0
// 调用本函数前需要对集合做排序，目的是让值相同的元素在位置上相邻，方便做树层去重
void backtracking(vector<int> nums, int targetSum, int sum, int startIndex, vector<int> used)
{
    // 终止条件
    if (sum > targetSum) return;
    if (sum == targetSum) 
    {
        res.push_back(path);
        return;
    }
    
    // 单层搜索逻辑
    // for循环是在同一层遍历各个节点，因此接下来就要写树层去重的逻辑
    for (int i = startIndex; i < nums.size(); i ++ ) 
    {
        // 树层去重, i > 0的目的是让i - 1 >= 0，也可以写作i > startIndex
        // used[i - 1] == 0对应于上面树的情况，就是第1个1没用，直接用了第2个1，此时重复读取，需要树层去重
        // 若nums[i] == nums[i - 1] && used[i - 1] == 1，则说明是树枝的状态，由于不需要树枝去重，所以此时不需要去重
        // 后续在回溯算法中遇到去重问题并使用used数组时，基本都是这种写法
        if (i > startIndex && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;
        // 收集元素
        path.push_back(nums[i]);
        sum += nums[i];
        used[i] = 1;
        // 递归
        backtracking(nums, targetSum, sum, i + 1, used);
        // 回溯
        path.pop_back();
        sum -= nums[i];
        used[i] = 0;
    }
}

可以用used数组进行去重，也可以用startIndex进行去重，这里不再深入讲解。用startIndex去重比较抽象，因此理解用used数组去重即可，更易于理解且通用。本题的关键在于理解去重的思路。

本题的完整代码如下所示：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& candidates, int target, int s, int startIndex, vector<int> used)
    {
        // 终止条件
        if (s > target) return;
        if (s == target) 
        {
            res.push_back(path);
            return;
        }

        // 单层搜索逻辑
        for (int i = startIndex; i < candidates.size(); i ++ )
        {
            // 树层去重
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0) continue;
            // 处理节点
            path.push_back(candidates[i]);
            used[i] = 1;
            s += candidates[i];

            // 递归
            backtracking(candidates, target, s, i + 1, used);

            // 回溯
            path.pop_back();
            used[i] = 0;
            s -= candidates[i];
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        // used数组用于标记candidates数组中的元素是否使用过，因此used数组大小应该与candidates数组大小保持相同
        vector<int> used(candidates.size(), 0); 
        sort(candidates.begin(), candidates.end()); // 别忘记排序
        backtracking(candidates, target, 0, 0, used);
        return res;
    }
};

时间复杂度: $O(n \times 2^n)$。同77.组合和39.组合总和。
空间复杂度：$O(n)$。原因：树的最大深度为n（同candidates数组的长度）。

131.分割回文串

aab。有两种分割方案：aa|b和a|a|b。本题要求我们返回所有的分割方案。如何使用回溯算法解决这个问题？

分割问题和组合问题非常相似。例如abcdef，对组合问题，如果选择了a，则在bcdef中选择下一个字母；如果选择了b，则在cdef中选择下一个字母。同理，对于分割问题，如果分割了a，则接下来分割bcdef。再分割b，则接下来分割cdef。接下来画分割问题的树形结构。

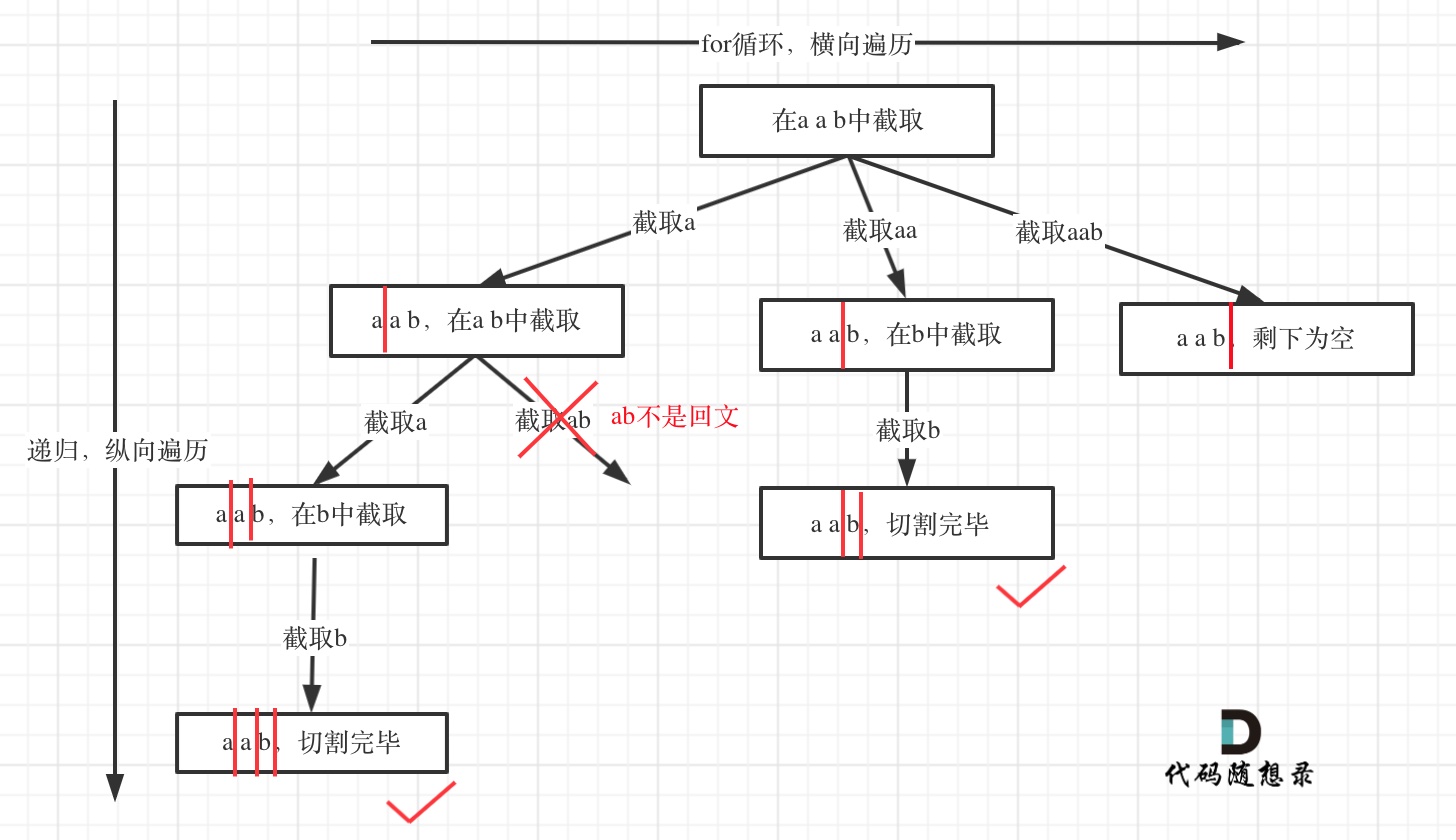
切割线到了字符串的末尾，则切割完毕。结果都在叶子节点。画树形结构较为简单，具体的代码实现中有几个难点，现在开始写具体的代码：

vector<string> path;
vector<vector<string>> res;

// 注意传入的变量类型是const string，再加上引用
// startIndex控制下一次切割的位置
void backtracking(const string& s, int startIndex)
{
    // 终止条件
    // 切割线到字符串的末尾，则终止
    // 切割线用startIndex表示
    if (startIndex >= s.size()) 
    {
        // 将判断是否是回文的逻辑放入单层搜索的逻辑中
        // 因此终止条件中的path都是符合回文条件的
        res.push_back(path);
        return;
    }
    
    // 单层搜索的逻辑
    for (int i = startIndex; i < s.size(); i ++ )
    {
        // 如何用代码表示切割出的子串
        // 切割的子串：[startIndex, i]，左闭右闭的区间
        // 用于判断是否回文的函数
        if (isPalindrome(s, startIndex, i)) // 传入字符串，子串的起始位置，子串的终止位置
        {
            path.push_back(子串); // 是回文，则将子串放入path中
        }
        else continue;
        // 递归
        backtracking(s, i + 1); // 下一层切割点从上一层切割点的下个位置开始，否则会重复
        // 回溯
        path.pop_back();
    }
}

isPalindrome函数用双指针算法可以轻松实现。注意本题的两个细节：

• startIndex是切割线

• 如何表示子串的范围：[startIndex, i]

完整的代码如下所示：

class Solution {
public:
    vector<string> path;
    vector<vector<string>> res;

    // 判断[start, end]是否是回文子串
    bool isPalindrome(const string& s, int start, int end)
    {
        for (int i = start, j = end; i <= j; i ++ , j -- )
            if (s[i] != s[j])
                return false;
        return true;
    }

    void backtracking(const string& s, int startIndex)
    {
        // 终止条件
        if (startIndex >= s.size()) 
        {
            res.push_back(path);
            return;
        }

        // 单层搜索逻辑
        for (int i = startIndex; i < s.size(); i ++ )
        {
            // 是回文子串，则将其加入path中
            if (isPalindrome(s, startIndex, i))
                path.push_back(s.substr(startIndex, i - startIndex + 1));
            else continue;

            // 递归
            backtracking(s, i + 1);

            // 回溯
            path.pop_back();
        }
    }

    vector<vector<string>> partition(string s) {
        backtracking(s, 0);
        return res;
    }
};

• 时间复杂度: $O(n \times 2^n)$，时间复杂度同77.组合、39.组合总和、40.组合总和II。

• 空间复杂度: $O(n^2)$，原因解释如下：

  1. 递归栈的空间：最深的递归发生在当字符串每个字符都被分割时，因此递归深度最大为$n$（其中$n$是字符串的长度）。每一层递归需要保存当前索引和路径，这些额外的空间可以认为是常数级别的。
  2. 路径存储空间 (path 和 res):
     • path 变量在最坏情况下（每个字符都独立成一个回文串时）会存储$n$个元素。
     • res 变量存储的是所有可能的分割方案。在极端情况下，如输入字符串完全由相同字符组成（例如 “aaaa”），分割方案的数量和其中每个方案的长度都可能接近$n$。但通常来说，我们只计算这个变量直接占用的空间，即指针或引用的空间，这通常也是$O(n^2)$，因为每个回文分割的保存都可能需要一个长度为 的$n$字符串的复制。
  3. 辅助空间：
     • 检查回文所用的额外空间是常量级的，不随输入大小变化。

  将以上所有考虑结合，整个算法的空间复杂度主要由存储所有分割方案的数组 res 决定。由于每个分割方案可能包含多个字符串，而每个字符串又可能需要$O(n)$的空间，因此在最坏情况下，这部分的空间复杂度为$O(n⋅k)$，其中 $k$是分割方案的数量，这在极端情况下可以达到$O(n^2)$。

心得与备忘录

39.组合总和

1. 本题通过target来限制树的深度，而77. 组合通过组合中元素的个数来限制树的深度。
2. 本题是集合里元素可以用无数次，那么和组合问题的差别，其实仅在于startIndex上的控制。本题若是想不重不漏，则下一层遍历的起始位置应该与上一层取出的数相同。而对于组合问题，下一层遍历的起始位置应该是上一层取出的数的下一个（因为组合问题中的元素不能重复使用）。
3. 本题的时间复杂度：$O(n \times 2^n)$，空间复杂度：$O(target)$。
4. 本题可以进行剪枝操作。具体来说，是对for循环进行剪枝。对candidate数组进行排序后，若某个分支的和大于target，那么就没必要对其后面的分支进行搜索了。体现在代码上，就是对总集合排序之后，如果下一层的sum（就是本层的sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。本题的剪枝不好想，要多加注意。

40.组合总和II

1. 本题的难点：集合有重复元素，但组合不能重复。

2. 本题需要对组合去重，但不能在搜索完整棵树后用哈希法去重，容易超时。需要在搜索的过程中去重，这需要用到used数组。其中用过的元素标记为1，没用过的元素标记为0。

3. 去重：只需要树层去重（树的同一层若两元素值相同，则右侧的值所在的路径必然被包含在左侧的值所在的路径中），不需要树枝去重（集合中的元素值可以相同，每个元素均可以使用一次，因此不需要对树枝去重）。

4. 本题不可忽视的几个细节：

   • 集合需要进行排序，这是为了将值相同的元素放在集合中相邻的位置，便于树层去重

   • used数组的大小需要与candidates数组保持相同，因为其是用来标记candidates数组中元素的使用情况的

   • 注意树层去重的代码的写法，建议结合实际例子（实现中的图片）进行理解

     // 树层去重
     if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0) continue;

     • candidates[i] == candidates[i - 1] && used[i - 1] == 0说明同一树层上相邻的两个元素相同，此时需要进行树层去重
     • used[i - 1] == 1，说明同一树枝上的candidates[i - 1]被使用过（同一树枝从上往下遍历，未进行回溯，因此candidates[i - 1]始终被标记为被使用过，即used[i - 1] = 1）
     • used[i - 1] == 0，说明同一树层上的candidates[i - 1]被使用过（同一树层从左往右经历过回溯的过程：先对candidates[i - 1]所在的树枝从上往下遍历，然后回溯，再对candidates[i]所在的树枝从上往下遍历。在回溯的过程中，candidates[i - 1]被重新标记为未被使用过，即used[i - 1] = 0）

5. 本题的去重代码不好写，同时细节较多需要注意。因此本题容易写错，需要时常复习。

6. 后续在回溯算法中遇到去重问题并使用used数组时，基本都是这种写法：if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0) continue;。

7. 本题也可以用startIndex进行去重，但比较难理解，因此不要求掌握。

8. 本题可以像39.组合总和一样进行剪枝操作，只需要在for循环中对i加上限制条件：s + candidates[i] <= target即可。

131.分割回文串

1. 首先，切割问题其实本质和组合问题是相同的。

   组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…..。接着选取一个b后，再从cdef中再去选取第二个，以此类推。

   切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…..。接着从b那里切下去，在cded中再去切割第二段，以此类推。

   可以观察本题的树形结构图，能够更加直观地理解切割问题和组合问题的相似。

2. 什么是切割线？

   递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线。

3. 终止条件：切割线startIndex移动到了字符串的末尾，即startIndex >= s.size()

4. 如何截取子串？[startIndex, i]之间的字符串就是子串。用substr函数截取即可。需要判断子串是否是回文串，是则放入path中，不是则continue。

5. 使用最简单的双指针算法即可写出判断字符串是否是回文串的函数。

6. 本题的空间复杂度$O(n^2)$。是极端情况下的空间复杂度，原因参见本题的实现部分。

7. 从主函数传入的参数，在定义其他函数时若需要这个参数，则需要将其设置为const类型。目的是防止其他函数对这个参数的修改，同时向函数的用户清楚地表明这个参数是用来输入数据的。不加const不影响代码的正常运行，但加了const后代码更加规范。