YifanChen's Blog

一个专注技术的新手程序员

0%

Day 27 Leetcode 93, 78, 90

发表于 更新于 分类于

链接

93.复原IP地址
78.子集
90.子集II

知识

93.复原IP地址

  1. cpp中的string是有pop_back方法的，用于弹出字符串中的最后一个元素。

  2. 字符串中在i的后面插入一个逗点

    1
    s.insert(s.begin() + i + 1 , '.');

  3. 删除特定位置处的逗点

    1
    s.erase(s.begin() + i + 1);

初次尝试

93.复原IP地址

我尝试按照131.分割回文串的思路做本题，也写出了相应的代码，但运行结果和答案相差很大，而且代码非常复杂。我来看看卡尔的解法，看看如何写出正确而简单地处理这种字符串类型的回溯题的代码。

78.子集

据卡尔说，子集问题，就是收集树形结构中，每一个节点的结果。 整体代码其实和回溯模板都是差不多的。 对于本题的树形结构，我有一个想法：以1, 2, 3为例，首先选中1前面的空位，则要收集空和123。然后选中1，则要收集1和23。然后选中2，则要收集2和13。然后选中3，则要收集3和12。共有8个子集。但本题的代码我写不出来，直接看卡尔的视频讲解。

90.子集II

本题是40.组合总和II再加上78.子集。利用40题的去重办法（树层去重，用used数组，即if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0)），利用78题的子集问题的解法（主要是在所有节点而不仅仅是叶子节点上收集答案）。据此，我独立写出了本题的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, int startIndex, vector<int>& used)
    {
        res.push_back(path);

        // 终止条件
        if (startIndex >= nums.size()) return;

        // 单层递归逻辑
        for (int i = startIndex; i < nums.size(); i ++ )
        {
            // 树层去重
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;
            // 处理节点
            path.push_back(nums[i]);
            used[i] = 1;
            // 递归
            backtracking(nums, i + 1, used);
            // 回溯
            path.pop_back();
            used[i] = 0;
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<int> used(nums.size(), 0);
        sort(nums.begin(), nums.end()); // 一定记得要对nums排序
        backtracking(nums, 0, used);
        return res;
    }
};

实现

93.复原IP地址

合法的IP地址：

  • 每个整数位于 0 到 255 之间组成
  • 数字前不能有0，即不能有先导0
  • 不能出现非0-9的字符

因此本题不仅需要对字符串进行切割，还要对子串进行合法性的判断。本题在回溯算法的切割问题中是一道较有难度的题。做了131.分割回文串后，再来做本题，会易于理解一些。使用回溯算法暴力枚举分割的每一种情况。画树形结构图。

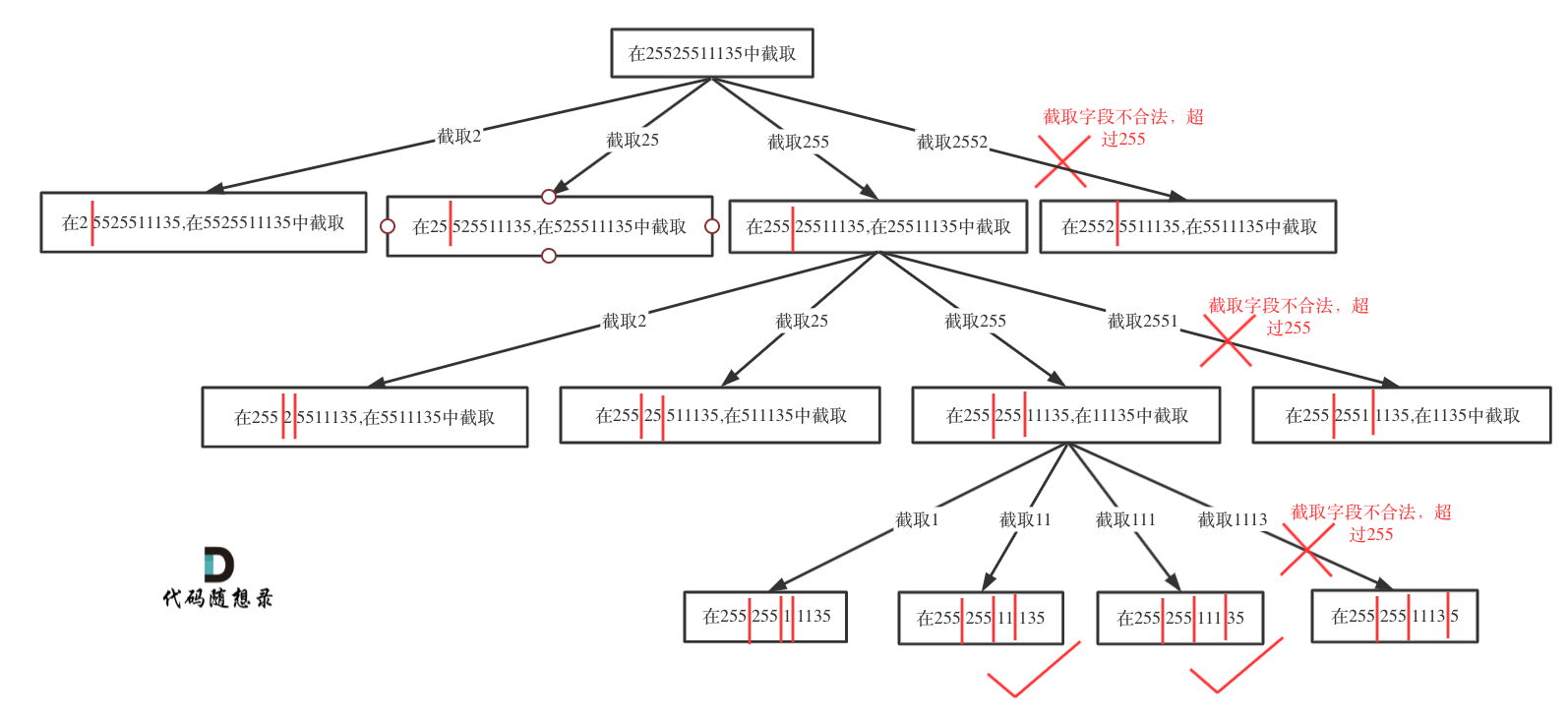
20201123203735933.png

画出了上述树形图后，写代码还会有疑惑：

  • 如何模拟切割线

  • 怎么固定切割线，再在剩余的字符串中进行切割

  • 切割出的子串如何表达

接下来写具体的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
vector<string> res;

// startIndex表示下一层递归切割的位置，即切割线
// 一个IP需要有三个逗点进行分割，pointSum用于统计逗点的数量, pointSum决定了树的深度
void backtracking(string& s, int startIndex, int pointSum)
{
    // 终止条件
    // 每次加逗点，都是对其前面的子串做合法性判断
    // 此时还需要专门对最后一个子串做合法性判断，最后一个子串合法了，才能将整个IP地址加入结果集中
    // isvalid用于判断一个子串是否合法：数字前不能有0，数字在0-255之间，子串中不能有非法字符
    if (pointSum == 3) {
        if (isvalid(s, startIndex, s.size() - 1)) // 左闭右闭
        {
            res.push_back(s); // s会在后面被修改，具体来说是被切割并加上逗点
            return;
        }
    }
    
    // 单层搜索逻辑
    for (int i = startIndex; i < s.size(); i ++ )
    {
        // 切割后，对产生的第一个子串的合法性进行判断。子串的区间：[startindex, i]
        if (isvalid(s, startIndex, i))
        {
        	  // 进入下一层递归前，需要在子串后面加上逗点
            // 将.插入到s.begin() + i的后面，故传入的参数是s.begin() + i + 1
            s.insert(s.begin() + i + 1, '.');
            pointSum += 1; // 逗点数量+1
            
            // 递归
            // 由于给字符串s额外加了一个逗点，因此是i + 2（本来是i + 1）
            backtracking(s, i + 2, pointSum);
            
            // 回溯
            s.erase(s.begin() + i + 1); // 删除s中插入的逗点
            pointSum -= 1;        
        }
    }
}

上述代码的精妙之处在于，就是在原来的字符串s的基础上进行修改，修改就是在合适的位置上添加逗点。本题的关键在于如何模拟切割的过程。切割的过程本质上和组合问题的取数的过程是一样的。另外还需要对子串进行合法性的判断，子串是[startIndex, i]。子串合法后再加上逗点。

根据上述核心代码，我独立写出了解决本题的完整的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
// 直接在s的基础上添加逗号，得到可能的IP地址
class Solution {
public:
    vector<string> res;

    // 判断区间[start, end]的合法性
    // 三个要求：1. 没有非数字的字符
    // 2. 在0-255之间
    // 3. 没有先导0
    bool isvalid(string& s, int start, int end)
    {
        if (start > end) return false;
        
        string tmp = s.substr(start, end - start + 1);

        // 先导0
        if (tmp.size() > 1 && tmp[0] == '0') return false;

        int sum = 0;
        int d = 1;

        for (int i = tmp.size() - 1; i >= 0; i -- )
        {
            // 非数字的字符
            if (tmp[i] < '0' || tmp[i] > '9') return false;
            sum += (tmp[i] - '0') * d;
            d = d * 10;
            if (sum > 255) return false;
        }
        return true;
    }

    // startIndex为分割线，dotSum为逗点数目
    void backtracking(string& s, int startIndex, int dotSum)
    {
        // 终止条件
        if (dotSum == 3)
        {
            // 对第四段(s的最后一段)做合法性判断
            if (isvalid(s, startIndex, s.size() - 1))
            {
                res.push_back(s);
            }
            return;
        }
        
        // 单层搜索逻辑
        // 区间[startIndex, i]
        for (int i = startIndex; i < s.size(); i ++ )
        {
            // 对区间合法性进行判断
            if (isvalid(s, startIndex, i))
            {
                // 合法，则插入逗点
                s.insert(s.begin() + i + 1, '.');
                dotSum ++ ;

                // 递归，本区间终止于i, 故下一个区间开始于i + 2
                backtracking(s, i + 2, dotSum);

                // 回溯
                s.erase(s.begin() + i + 1);
                dotSum -- ;
            }
        }
    }

    vector<string> restoreIpAddresses(string s) {
        backtracking(s, 0, 0);
        return res;
    }
};

isvalid函数可以写的更简洁更自然：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool isvalid(string& s, int start, int end)
{
    if (start > end) return false;

    // 先导0
    if (s[start] == '0' && start != end) return false;

    int num = 0;
    for (int i = start; i <= end; i ++ )
    {
        // 非数字字符
        if (s[i] < '0' || s[i] > '9') return false;
        // 在0-255之间
        num = num * 10 + s[i] - '0';
        if (num > 255) return false;
    }
    return true;
}
  • 时间复杂度: $O(3^4)$，IP地址最多包含4个数字，每个数字最多有3种可能的分割方式（1位，2位，3位）；则搜索树的最大深度为4，每个节点最多有3个子节点（对应每个数字可能是1位，2位，3位的情况）。
  • 空间复杂度: $O(n)$，原因如下：
    • 递归栈：递归的深度固定，最多为4，因为IP地址由四部分组成。但这并不直接决定空间复杂度，因为递归深度很小。
    • 存储当前解：在递归过程中，需要存储当前正在构建的IP地址，这需要额外的空间。此外，每次递归调用时，都可能创建字符串的子串来表示IP地址的某一部分。字符串的最大长度为输入字符串的长度n，因此需要额外的空间来存储这些子串。
    • 输出解的集合：输出的解的数量并不直接影响空间复杂度的理论计算，但实际上会使用额外空间来存储所有可能的IP地址。然而，这些空间通常不计入空间复杂度计算中，因为它不依赖于递归过程中的临时存储需求。

78.子集

之前讲的组合问题、分割问题，我们都是在树形结构的叶子节点上收获结果，因此在终止条件处收获结果。可以画出如下的树形结构：

78.子集

观察如上树形结构，发现我们想收获的结果其实在每一个节点中。因此不是在终止条件中收获结果，而是每进入一层递归就将单个结果放入结果集中。现在开始对着树形结果写代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 一维数组存放单个结果
vector<int> path;
// 二维数组作为结果集
vector<vector<int>> res;

// startIndex：下一层递归从哪里开始取数
void backtracking(vector<int> nums, int startIndex)
{
    // 每进入一层递归，都要将当前的path放入结果集中
    // 因为要将叶子节点的集合放入结果集中，然后再结束，因此先有本逻辑，再有终止条件
    res.push_back(path); 
    
    // 终止条件：走到叶子节点，叶子节点的剩余集合都为空
    // 本终止条件可以不写，因为单层搜索逻辑中的for循环已经对startIndex的大小进行了限制
    if (startIndex >= nums.size()) return;
    
    // 单层搜索逻辑
    for (int i = startIndex; i < nums.size(); i ++ )
    {
        // 每进入一层递归，都要收获当前节点的结果，放入单个结果数组中
        path.push_back(nums[i]);
        // 进入下一层递归
        backtracking(nums, i + 1);
        // 回溯
        path.pop_back();
    }
}

不写终止条件的写法如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, int startIndex)
    {
        res.push_back(path);

        for (int i = startIndex; i < nums.size(); i ++ )
        {
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
        return;
    }

    vector<vector<int>> subsets(vector<int>& nums) {
        backtracking(nums, 0);
        return res;
    }
};

90.子集II

与78的区别：给的集合中允许有重复的元素，因此需要对重复子集去重。本题的关键在于去重，本题是子集+组合总和II（树层去重）的结合，并没有新的知识点。

本题的树形结构。used数组用于记录某个元素是否出现过。因为去重要让大小相邻的元素挨在一起，因此需要先对数组进行排序。本题的去重是树层去重（树层上相邻的元素如果相等，则不能重复取，否则会得到重复的子集），树枝不需要去重。

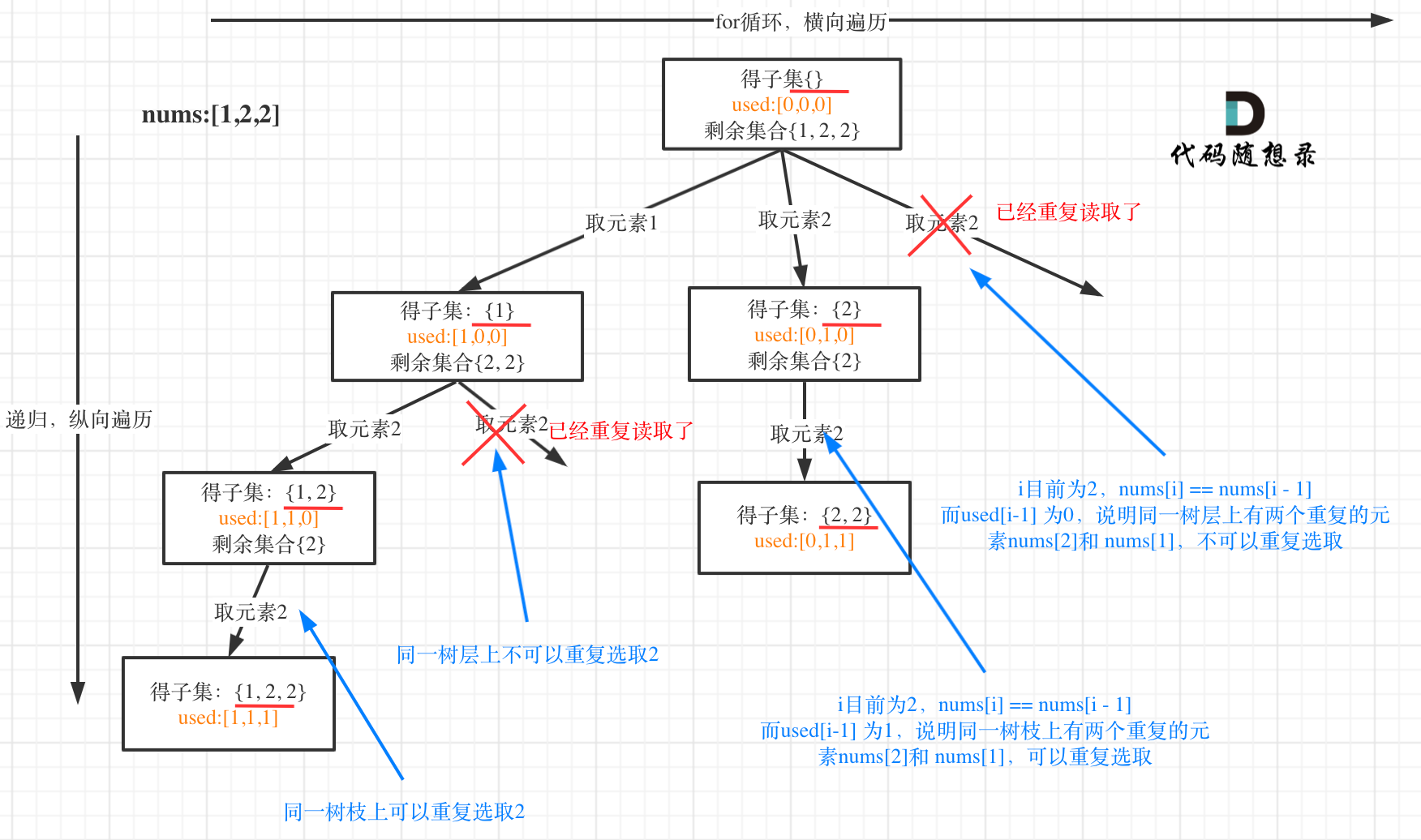
90.子集II

现在开始写代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
vector<int> path; // 单个结果
vector<vector<int>> res; // 结果集

void backtracking(vector<int>& nums, int startIndex, vector<int>& used)
{
    // 终止条件不需要写，在for循环中实际上已经限制了startIndex的大小
    res.push_back(path); // 收获结果，需要在每个节点都收获结果
    
    // 单层递归逻辑
    for (int i = startIndex; i < nums.size(); i ++ )
    {
        // 树层去重, used[i - 1] == 0意味着第i - 1个元素是第i个元素的回溯
        if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] = 0) continue;
        // 处理节点
        path.push_back(nums[i]);
        used[i] = 1;
        // 递归
        backtracking(nums, i + 1, used);
        // 回溯
        path.pop_back();
        used[i] = 0;
    }
}

回溯中的去重逻辑都这么写。本题去重也可以用startIndex和i进行比较来实现，但这种去重写法并不通用，遇到排列问题时依然要用used数组的写法进行去重。去重的写法掌握used数组写法即可。

本题的时间和空间复杂度和78相同。时间复杂度: $O(n\times2^n)$，空间复杂度: $O(n)$。

本题也可以用哈希法去重，但时间复杂度更高，虽然也能够通过所有测试样例且不超时，代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, int startIndex)
    {
        res.push_back(path);
        unordered_set<int> s;

        for (int i = startIndex; i < nums.size(); i ++ )
        {
            // set去重
            if (s.find(nums[i]) != s.end()) continue;

            // 处理节点
            s.insert(nums[i]);
            path.push_back(nums[i]);
            // 递归
            backtracking(nums, i + 1);
            // 回溯
            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end()); // set去重依然需要排序
        backtracking(nums, 0);
        return res;
    }
};

因此，本题的去重写法有三种：

  • used数组去重
  • startIndex去重
  • set去重

掌握第一种即可。第一种是思路最清晰也最通用的。

本题像78一样，也可以不写终止条件，因为startIndex的大小在for循环中已经得到了限制。精简版本的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, int startIndex, vector<int>& used)
    {
        res.push_back(path);

        for (int i = startIndex; i < nums.size(); i ++ )
        {
            // 去重
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;
            // 处理节点
            path.push_back(nums[i]);
            used[i] = 1;
            // 递归
            backtracking(nums, i + 1, used);
            // 回溯
            path.pop_back();
            used[i] = 0;
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<int> used(nums.size(), 0);
        sort(nums.begin(), nums.end());
        backtracking(nums, 0, used);
        return res;
    }
};

心得与备忘录

93.复原IP地址

  1. 本题是131.分割回文串的加强版。因为和131同样是用回溯法求解的分割问题，所以基本原理是相同的，比如startIndex用于作为分割线，分割的区间是[startIndex, i]。
  2. 本题的终止条件和131有显著地不同。131的终止条件是startIndex移动到字符串的末尾，而本题的终止条件是添加了3个逗点，且最后一段区间是合法的。3个逗点的终止条件也限制了树的深度。
  3. 一般处理字符串的问题都比较复杂。本题对字符串处理的精妙之处在于直接在原本的字符串s上进行修改，添加逗点，作为分隔符从而得到合法的IP地址。本题还用到了两个和字符串有关的STL，分别是insert和erase函数。
  4. 本题对区间合法性的判断较为复杂，共有3个要求：
    • 段位以0为开头的数字不合法
    • 段位里有非正整数字符不合法
    • 段位如果大于255了不合法
    • 段位若大于255，则立即判断为不合法，return false。若完成for循环后再对num进行判断，可能出现整数型变量溢出
  5. 本题的时间复杂度：$O(3^4)$，空间复杂度：$O(n)$
  6. 本题的细节比较多，比较容易写错，属于回溯法解决分割问题中的难题，需要不断复习。

78.子集

  1. 子集是收集树形结构中树的所有节点的结果。而组合问题、分割问题是收集树形结构中叶子节点的结果。
  2. 子集也是一种组合问题，因为它的集合是无序的，子集{1,2}和子集{2,1}是一样的。那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始。
  3. 先收集结果集，再写终止条件的原因：当递归到叶子节点时，要先将叶子节点的结果放入结果集中，再终止，因此先写收集结果集的逻辑，再写终止条件。否则叶子节点的结果无法被放入结果集中。
  4. 本题也可以不写终止条件，因为单层递归逻辑的for循环中实际上限制了startIndex的大小，因此最后return即可。但初学者还是建议写终止条件，和标准的回溯模板保持一致。
  5. 本题的时间复杂度: $O(n\times2^n)$，空间复杂度: $O(n)$。时间和空间复杂度的分析同77.组合。

90.子集II

  1. 本题是40.组合总和II与78.子集这两题的结合。

  2. 40的精华在于去重（树层去重），78的精华在于在每个节点处都收集结果（而不是像组合、分割问题那样在叶子节点，即终止条件处收集结果），而是在递归函数的开始处（进入递归相当于进入一个节点）收集结果。本题结合了两题的精华。

  3. 树层去重掌握used数组写法即可，具体代码为：

    1
    if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;
  4. 树层去重前，需要对nums数组进行排序。
  5. 本题的时间和空间复杂度和上一题（78）相同。
  6. 去重共有三种写法，掌握思路最清晰也最通用的used数组写法即可。
  7. 本题像78一样，也可以不写终止条件，因为startIndex的大小在for循环中已经得到了限制。