LeetCode problems prepared for a TikTok interview

34. 在排序数组中查找元素的第一个和最后一个位置

本题是整数二分的加强版。本题的要点为：

写两个函数，分别寻找target的左边界和右边界。本题的区间定义为左闭右闭。
寻找左边界，说明target在[left, mid]之间，因此在[left, mid]中更新左边界。寻找右边界，说明target在[mid, right]之间，因此在[mid, right]中更新右边界。
寻找左边界，就要在nums[mid] == target的时候更新right，然后将right赋给左边界。寻找右边界，就要在nums[mid] == target的时候更新left，然后将left赋给右边界。
实际上的左右边界是mid，而非right和left，因此在主函数中需要将左边界+1，恢复为mid；将右边界-1，也恢复为mid。也可以直接让左右边界是mid，这样就不需要加1减1，参见我的第二种写法。

target的三种情况：

target在数组范围的右边或者左边
target 在数组范围中，且数组中存在target

target 在数组范围中，且数组中不存在target

// 左闭右闭写法
class Solution {
public:
    // 寻找左边界
    // 说明target在[left, mid]之间
    int findLeftBorder(vector<int>& nums, int target)
    {
        int leftBorder = -2;
        int left = 0, right = nums.size() - 1;

        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            // 在[left, mid]中更新左边界
            if (nums[mid] >= target)
            {
                right = mid - 1;
                leftBorder = right;
            }
            else left = mid + 1;
        }
        return leftBorder;
    }

    // 寻找右边界
    // 说明target在[mid, right]之间
    int findRightBorder(vector<int>& nums, int target)
    {
        int rightBorder = -2;
        int left = 0, right = nums.size() - 1;

        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) right = mid - 1;
            // 在[mid, right]中更新右边界
            else 
            {
                left = mid + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }

    vector<int> searchRange(vector<int>& nums, int target) {
        int leftBorder = findLeftBorder(nums, target);
        int rightBorder = findRightBorder(nums, target);

        // target在数组范围的右边或者左边
        if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
        // target 在数组范围中，且数组中存在target
        if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
        // target 在数组范围中，且数组中不存在target
        return {-1, -1};
    }
};

我写出了以下的变式代码。在这个代码里，通过mid来更新左右边界。这样若找到了左右边界，则直接返回左右边界即可，不需要做加1减1的操作。

// 左闭右闭写法
class Solution {
public:
    // 寻找左边界
    // 说明target在[left, mid]之间
    int findLeftBorder(vector<int>& nums, int target)
    {
        int leftBorder = -2;
        int left = 0, right = nums.size() - 1;

        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            // 在[left, mid]中更新左边界
            if (nums[mid] >= target)
            {
                right = mid - 1;
                leftBorder = mid;
            }
            else left = mid + 1;
        }
        return leftBorder;
    }

    // 寻找右边界
    // 说明target在[mid, right]之间
    int findRightBorder(vector<int>& nums, int target)
    {
        int rightBorder = -2;
        int left = 0, right = nums.size() - 1;

        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) right = mid - 1;
            // 在[mid, right]中更新右边界
            else 
            {
                left = mid + 1;
                rightBorder = mid;
            }
        }
        return rightBorder;
    }

    vector<int> searchRange(vector<int>& nums, int target) {
        int leftBorder = findLeftBorder(nums, target);
        int rightBorder = findRightBorder(nums, target);

        // target在数组范围的右边或者左边
        if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
        // target 在数组范围中，且数组中存在target
        if (rightBorder - leftBorder >= 0) return {leftBorder, rightBorder};
        // target 在数组范围中，且数组中不存在target
        return {-1, -1};
    }
};

278.第一个坏版本

我独立写出了以下代码：

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        int left = 1, right = n;

        while (left < right)
        {
            int mid = left + (right - left) / 2;
            if (isBadVersion(mid) == 0) left = mid + 1;
            else right = mid;
        }
        return left;
    }
};

在本题中，尽管是左闭右闭的写法，但循环的条件应该为left < right，因为当left = right时，实际上就锁定了第一个坏版本，循环就应当结束。这种题目当出现超时，要着重检查是不是循环的条件不对。

和本题同样的题目：输入一个数组，比如[0, 0, 0, 1, 1, 1, 1]，找到第一个为1的数的下标，代码如下所示：

#include <iostream>
#include <vector>
using namespace std;

int firstBadVersion(vector<int> arr)
{
    int left = 0, right = arr.size() - 1;

    while (left < right)
    {
        int mid = left + (right - left) / 2;
        if (arr[mid] == 1) right = mid;
        else left = mid + 1;
    }
    return left;
}

int main()
{
    vector<int> arr = {0, 0, 0, 1, 1, 1, 1, 1};
    cout << firstBadVersion(arr) << endl;
    return 0;
}

27. 移除元素

本题直接采用（快慢）双指针解法即可。一遍过，但需要注意不要在for循环中重复定义指针j。本题的暴力做法甚至比双指针做法更复杂，也更容易写错。相向双指针做法暂时不用管。

977.有序数组的平方

暴力解法非常简单，也能通过测试。我先在纸上模拟了双指针的过程，然后独立写出了如下的双指针代码，时间和空间复杂度都是$O(n)$。

// 双指针经典题
class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int size = nums.size() - 1;
        vector<int> res(nums.size(), 0);

        for (int i = 0, j = size; i <= j; )
        {
            if (nums[i] * nums[i] <= nums[j] * nums[j]) 
            {
                res[size] = nums[j] * nums[j];
                j -- ;
                size -- ;
            }
            else
            {
                res[size] = nums[i] * nums[i];
                i ++ ;
                size -- ;
            }
        }

        return res;
    }
};

不要追求把代码写得过度简洁，而导致可能的问题，宁可把代码写长一些，也要让代码清楚地表达算法思想。

209.长度最小的子数组

一时想不起来具体怎么写了，只记得遍历整个数组的同时，有数划入窗口，该数被累加到和中，有数划出窗口，则该数被从和中减去。看了我自己的笔记后，我独立写出了以下的代码：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int len = INT_MAX;
        int s = 0; // 滑动窗口的和
        int i = 0; // 起始位置

        // j为终止位置
        for (int j = 0; j < nums.size(); j ++ )
        {
            s += nums[j]; // 终止位置划入

            while (s >= target)
            {
                int sub = j - i + 1;
                if (sub < len) len = sub;
                s -= nums[i]; // 起始位置从和中滑出
                i ++ ; // 起始位置从滑动窗口中滑出
            }
        }
        if (len == INT_MAX) return 0;
        else return len;
    }
};

需要注意：

i为起始位置，j为终止位置
循环中，终止位置先划入。若和大于等于目标值，则先更新最小长度，再将起始位置划出。
起始位置的值需要先从和中滑出，起始位置再从滑动窗口中滑出。顺序不可颠倒。
for循环中是while循环，而非if判断
数组中的每个元素至多被滑入一次再滑出一次，因此时间复杂度是$O(2n)$，即$O(n)$。

59.螺旋矩阵II

我记得本题是个模拟题。但实在记不得怎么做了，看以前的笔记。复习完后，我写出了本题的代码：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0));

        int i, j;
        int startx = 0, starty = 0;
        int offset = 1, cnt = 1;
        int loop = n / 2;

        while (loop -- )
        {
            for (j = starty; j < n - offset; j ++ )
                res[startx][j] = cnt ++ ;
            for (i = startx; i < n - offset; i ++ )
                res[i][j] = cnt ++ ;
            for (j = n - offset; j > starty; j -- )
                res[i][j] = cnt ++ ;
            for (i = n - offset; i > startx; i -- )
                res[i][j] = cnt ++ ;
            offset ++ ;
            startx ++ ;
            starty ++ ;
        }
        if (n % 2) res[n / 2][n / 2] = cnt;
        return res;
    }
};

需要注意：

画图理解（记住本图，就可以写出这道题的代码）：
顺时针转圈，转多少圈可以填满整个二维数组？从(0, 0)的位置开始转圈，终止的位置为中心(n/2, n/2)。每转一圈横纵坐标均加1，因此一共转了n/2圈。
切记遵守循环不变量原则，所有边都是左闭右开的。所以是j < n - offset，且offset的初始值为1，因为右边界是开的。
startx, starty, offset每转一圈都要加1。
定义二维数组的方式是将一位数组复制行数遍。
若n为奇数，则最后记得向二维数组的中心填入最后一个数。

189.旋转数组

首先我写出了可以正常运行但会超时的代码：

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        while (k -- )
        {
            reverse(nums.begin(), nums.end());
            reverse(nums.begin() + 1, nums.end());
        }
    }
};

不超时的代码我写不出来，看卡尔的讲解。

本题的代码如下所示：

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        k = k % nums.size();
        reverse(nums.begin(), nums.end());
        reverse(nums.begin(), nums.begin() + k);
        reverse(nums.begin() + k, nums.end());
    }
};

本题其实原理不难，类似于旋转字符串的题目，总结如下：

首先反转整个数组，这样在不考虑顺序的情况下，就将两段数字放在了正确的位置上。
然后反转前k个数，将前k个数的顺序调整正确。
最后反转剩下的数，将剩下的数的顺序调整正确。
需要注意的是，若k > nums.size()，则右移k % nums.size()即可，因为右移nums.size()次相当于没有改变原数组。
不要对nums.end()进行加减操作，nums.end()不指向一个特定的元素（不要下意识地以为其指向最后一个元素后面的紧邻的位置），对其进行加减操作会导致未定义的随机行为。对nums.begin()进行操作就没有这个问题。因此反转的第三步不要写成reverse(nums.end() - k - 1, nums.end())。

153.寻找旋转数组中的最小值

应该是先要将其恢复为有序的数组，然后返回有序数组的第一个元素即可。本题应该结合了二分法和旋转数组。我直接看题解吧。

虽然但是，本题用暴力做法也可以通过：

class Solution {
public:
    int findMin(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        return nums[0];
    }
};

上述算法的时间复杂度是O(nlogn)。用二分法应该可以将时间复杂度优化为O(logn)。

本题的二分做法如下所示：

// 左闭右闭写法
class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;

        // 循环的终止条件：left = right。此时必然已经找到了数组中的最小值
        while (left < right)
        {
            int mid = left + (right - left) / 2;
            // 中间数字大于右边数字，比如[3,4,5,1,2]，则左侧是有序上升的，最小值在右侧
            if (nums[mid] > nums[right]) left = mid + 1;
            // 中间数字小于右边数字，比如[6,7,1,2,3,4,5]，则右侧是有序上升的，最小值在左侧
            // 以[6, 7, 1, 2, 3, 4]为例，mid = 2, right = 2，即恰好在[left, mid]中取到最小值1
            // 若right = mid - 1，则[left, right]会错过最小值
            else if (nums[mid] < nums[right]) right = mid;
            // 中间数字等于右边数字，则说明数组中只有一个元素，返回该元素即可
            // 也可以直接写作else right = mid;
        }
        return nums[left];
    }
};

本题延续了二分法的思路和代码形式，但细节和二分法略有不同，需要注意复习。

本题的思路：

本题是左闭右闭写法，区间为[left, right]
数组中的最小值要么在数组的右侧，要么在数组的左侧
数组的最小值在数组右侧的情况：[3, 4, 5, 1, 2]。数组的最小值在数组左侧的情况：[6, 7, 1, 2, 3, 4, 5]
若数组的最小值在数组的右侧，由于nums[mid] > nums[right]，因此nums[mid]必然不可能是数组的最小值，因此left = mid + 1
对于剩下的情况，即nums[mid] <= nums[right]，数组的最小值在数组的左侧。由于可能存在nums[mid] = nums[right]的情况，因此nums[mid]可能是最小值，因此有right = mid
记住始终是nums[mid]和nums[right]比较。始终是中间和右边比！

本题的另一种思路（更推荐这种，因为这种思路可以推广到33）：

nums[mid]和nums[right]的关系可以分为大于，等于，小于三种情况
nums[mid] == nums[right]时，中间的数字等于最右边的数字，说明数组中只有一个元素，此时返回nums[left]即可，这种情况不需要考虑
nums[mid] > nums[right]时，例如[3, 4, 5, 1, 2]。数组的最小值在数组的右侧，nums[mid]必定不为最小值，因此有left = mid + 1
nums[mid] < nums[right]时，数组的最小值在数组的左侧。例如[6, 7, 1, 2, 3, 4, 5]，也有可能是[6, 7, 1, 2, 3, 4]，此时mid = 2, right = 2，即恰好在[left, mid]中取到最小值1。若right = mid - 1，则[left, right]会错过最小值，因此right = mid

154.寻找旋转数组中的最小值II

本题的思路：

延续上题的思路，nums[mid]和nums[right]的关系可以分为大于，等于，小于三种情况
nums[mid] > nums[right]和nums[mid] < nums[right]的情况同上
由于数组中可以有重复的元素，因此需要考虑nums[mid] == mums[right]的情况，例如[2,3,1,1,1]或者[4,1,2,3,3,3,3]。此时，重复值nums[right]可能是最小值，也可能最小值在重复值的左侧，因此right左移一位：right -= 1

本题的代码如下所示：

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;

        while (left < right)
        {
            int mid = left + (right - left) / 2;
            // [5, 6, 7, 1, 2]
            if (nums[mid] > nums[right]) left = mid + 1;
            // [7, 1, 2, 3, 4]
            else if (nums[mid] < nums[right]) right = mid;
            else right -= 1;
        }
        return nums[left];
    }
};

33.搜索旋转排序数组

我对本题的初步思路：先找到最小的那个点，然后分别对两段单调递增的区间用二分法进行搜索。根据这个原理，我独立写出了以下的代码：

class Solution {
public:
    // 二分查找有序数组中的数
    // 左闭右闭写法
    int searchTarget(vector<int>& nums, int left, int right, int target)
    {
        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) right = mid - 1;
            else if (nums[mid] < target) left = mid + 1;
            else return mid;
        }
        return -1;
    }

    int search(vector<int>& nums, int target) {
        // 先找到最小的数字, 下标为left
        int left = 0, right = nums.size() - 1;

        while (left < right)
        {
            int mid = left + (right - left) / 2;
            // nums[mid] nums[right], [4, 5, 6, 7, 0, 1, 2]
            if (nums[mid] > nums[right]) left = mid + 1;
            else right = mid;
        }

        int leftIndex = searchTarget(nums, 0, left - 1, target);
        int rightIndex = searchTarget(nums, left, nums.size() - 1, target);

        if (leftIndex == -1 && rightIndex == -1) return -1;
        else if (leftIndex == -1) return rightIndex;
        else if (rightIndex == -1) return leftIndex;
        return -1;
    }
};

时间复杂度也是$O(logn)$。

更简单的写法如下：

// 左闭右闭写法
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        
        // 本质是查找target，因此是小于等于。若是查找最小值，则是小于
        while (left <= right)
        {
            int mid = left + (right - left) / 2;

            // 第一种情况，直接找到
            if (nums[mid] == target) return mid;

            // 由于第一种情况已经讨论过nums[mid] == target，因此第二三种情况不用再讨论
            // 第二种情况，数组最小值在右侧, [left, mid]为有序
            if (nums[mid] > nums[right])
            {
                // target在[left, mid](有序)内
                if (target >= nums[left] && target < nums[mid]) right = mid - 1;
                // target在无序区间内
                else left = mid + 1;
            }

            // 第三种情况，数组最小值在左侧，[mid, right]为有序
            else
            {
                // target在[mid, right]区间内
                if (target > nums[mid] && target <= nums[right]) left = mid + 1;
                // target在无序区间内
                else right = mid - 1;
            }
        }
        return -1;
    }
};

分三种情况讨论：

直接在mid处找到target
数组最小值在右侧, [left, mid]为有序
- target在[left, mid]有序区间内
- target在剩余的无序区间内
数组最小值在左侧，[mid, right]为有序
- target在[mid, right]有序区间内
- target在剩余的无序区间内

81.搜索旋转排序数组II

本题依然可以用老思路：找到最小值点，将区间划分为两个单调区间，然后分别在两个单调区间中进行搜索。本题实际上不可以这样做，因为本题中数组的元素可以重复，可能存在不止一个最小值点。

看了答案后，发现本题有两种写法，第一种：在循环内部跳过数组左侧和右侧的重复元素：

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;

        while (left <= right) {
            // 跳过数组左侧的重复元素
            while (left < right && nums[left] == nums[left + 1]) left++;
            // 跳过数组右侧的重复元素
            while (left < right && nums[right] == nums[right - 1]) right--;

            int mid = left + (right - left) / 2;
            if (nums[mid] == target) return true;

            // 判断有序部分
            if (nums[mid] >= nums[left]) {  // 左侧有序
                if (target >= nums[left] && target < nums[mid]) {
                    right = mid - 1;
                } else {
                    left = mid + 1;
                }
            } else {  // 右侧有序
                if (target > nums[mid] && target <= nums[right]) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
        }
        return false;
    }
};

第二种，在循环外部直接删去数组尾部与数组头部重复的元素：

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        // 移除重复的末尾元素以减少干扰
        // 可以处理如下情况：[1, 0, 1, 1, 1], [1, 2, 2, 2, 2, 0, 1]
        // nums.front() == nums.back()时，可能数组右边有序，也可能左边有序
        // 也可写作nums[0] == nums[nums.size() - 1]
        while (nums.size() > 1 && nums.front() == nums.back()) nums.pop_back();

        int left = 0, right = nums.size() - 1;

        while (left <= right)
        {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target) return true;

            // [3, 4, 5, 1, 2]
            if (nums[mid] > nums[right])
            {
                // 有序区间[left, mid]
                if (target >= nums[left] && target < nums[mid]) right = mid - 1;
                // 无序区间[mid, right]
                else left = mid + 1;
            }
            else
            {
                // 有序区间[mid, right]
                if (target > nums[mid] && target <= nums[right]) left = mid + 1;
                // 无序区间[left, mid]
                else right = mid - 1;
            }
        }
        return false;
    }
};

注意：需要先移除重复的末尾元素以减少干扰，再给left和right赋值。

建议采用第二种写法，因为第二种写法相当于在33.搜索旋转排序数组的基础上仅仅添加了移除重复的末尾元素的代码。这道题相当与上一题区别在于这道题包含了重复元素，其实影响到的是，当左端点和右端点相等时，无法判断mid在左半边有序数组还是右半边有序数组，所以只需要一直pop直到左端点和右端点不相等就可以了。

442. 数组中重复的数据

448. 找到所有数组中消失的数字

只有当数字的范围和数组的大小相等，或者有一定偏移关系时，才可以用原地哈希。本题的数字范围1-n，本题的数组中有n个元素，数组下标的范围是0-n-1。这种原地哈希算法适用于和正整数有关，且数字范围和数组长度有关的题目里，映射之后能利用映射关系（下标和值一一对应）来找到解。

对于本题，本质就是将原数组的下标为nums[i] - 1处放上nums[i]，最终希望达到的效果是nums[nums[i] - 1] == nums[i]。本题的代码如下所示：

class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> res;

        // 将nums[i]放到下标为nums[i] - 1的位置上
        // 由于原来下标为nums[i] - 1的位置上可能有数，因此需要将该数暂存到nums[i]上
        // 之后可以通过while循环将再将该数放到合适的位置上去
        // 可以举例子来模拟，即可以弄清楚这个过程
        for (int i = 0; i < nums.size(); i ++ )
        {
            while (nums[nums[i] - 1] != nums[i])
            {
                int idx = nums[i] - 1;
                int tmp = nums[idx];
                nums[idx] = nums[i];
                nums[i] = tmp;
            }
        }

        for (int i = 0; i < nums.size(); i ++ ) 
        {
            // 若nums[i]上的数字不为i + 1，则说明该数字缺失，将其插入结果集中
            if (nums[i] != i + 1)
                res.push_back(i + 1);
        }

        return res;
    }
};

本题的精简注释版本如下所示：

class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> res;
        int n = nums.size();

        for (int i = 0; i < n; i ++ )
        {
            // 确保将nums[i]放到下标为nums[i] - 1的位置上
            while (nums[nums[i] - 1] != nums[i])
            {
                int idx = nums[i] - 1; // 即将占用的元素的下标
                int tmp = nums[idx]; // 暂存下标为idx处的元素，因为其即将被nums[i]占用
                nums[idx] = nums[i]; // 将nums[i]放到下标为nums[i] - 1的位置上
                nums[i] = tmp; // 将原来数组中下标为nums[i] - 1的数暂存到位置i
            }
        }

        for (int i = 0; i < n; i ++ )
            if (nums[i] != i + 1) res.push_back(i + 1);
            
        return res;
    }
};

while循环中的顺序：先写：

1 2	int idx = nums[i] - 1; nums[idx] = nums[i];

确保nums[i]被放在了下标为nums[i] - 1处。

再将原本下标为idx处的元素缓存下来，暂存到下标i处：

1 2	int tmp = nums[idx]; nums[i] = tmp;

由此构成完整的代码：

int idx = nums[i] - 1;
int tmp = nums[idx];
nums[idx] = nums[i];
nums[i] = tmp;

442. 数组中重复的数据

本题依然可以用448的原地哈希法完成，唯一地不同在于，448是将i + 1插入res数组中，本题是将nums[i]插入res数组中，举一个实际的例子即可理解为什么是将nums[i]插入结果集中。

class Solution {
public:
    vector<int> findDuplicates(vector<int>& nums) {
        vector<int> res;
        int n = nums.size();

        for (int i = 0; i < n; i ++ )
        {
            while (nums[nums[i] - 1] != nums[i])
            {
                int idx = nums[i] - 1;
                int tmp = nums[idx];
                nums[idx] = nums[i];
                nums[i] = tmp;
            }
        }

        for (int i = 0; i < n; i ++ )
        {
            if (nums[i] != i + 1) res.push_back(nums[i]);
        }
        return res;
    }
};

对原地哈希可进行总结：

情景：数组的长度为n，数组中元素的范围为[1, n]
若是找缺失的数字，则插入结果集的是索引下标+1；若是找出现了两遍的数字，则插入结果集的是元素的值nums[i]
使用代码块：
1
2
3
4
5
6
7
8
9
10
for (int i = 0; i < n; i ++ )
{
while (nums[nums[i] - 1] != nums[i])
{
int idx = nums[i] - 1;
int tmp = nums[idx];
nums[idx] = nums[i];
nums[i] = tmp;
}
}
对数组进行原地哈希后，数组中出现过的数字nums[i]会被重新放置在下标为nums[i] - 1的位置上。范围为[1, n]但数组中没出现过的数字nums[j]，其本来应该放置在下标为nums[j] - 1处，但由于没有出现过，现在下标为nums[j] - 1处放置了原数组中的重复元素。这是因为循环的条件nums[nums[i] - 1] != nums[i]，当未填满的位置填入了重复元素后，while循环也会终止。例如，对[4, 3, 2, 2, 3, 1]进行原地哈希，结果为[1, 2, 3, 4, 3, 2]，原数组中出现过的1, 2, 3, 4被放置在下标为0, 1, 2, 3的位置上，原数组中没有出现过5, 6，因此下标为4，5处放置了原数组中重复的元素2, 3。
原地哈希法的时间复杂度都为O(n)，空间复杂度都为O(1)
为什么是 O(n) 时间复杂度？

每个元素在整个过程中最多被处理两次（一次是放置在正确位置，一次是在最终遍历中检查），因此总体时间复杂度是 O(2n)==O(n)。

41. 缺失的第一个正数

本题的思路和448、442相同，只不过while循环多了限制条件，同时返回值时需要考虑一种特殊情况。

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();

        for (int i = 0; i < n; i ++ )
        {
            // 为避免nums[i] - 1超出索引的范围，需要对nums[i]的大小进行限制
            // 0 <= nums[i] - 1 <= n - 1，因此1 <= nums[i] <= n
            // 不需要对此范围之外的数进行操作，也无法用原地哈希法操作它们，因为它们会超出索引范围
            while (nums[i] >= 1 && nums[i] <= n && nums[nums[i] - 1] != nums[i])
            {
                // 这四行代码可以简写为swap(nums[nums[i] - 1], nums[i]);
                int idx = nums[i] - 1;
                int tmp = nums[idx];
                nums[idx] = nums[i];
                nums[i] = tmp;
            }
        }

        for (int i = 0; i < n; i ++ )
        {
            if (nums[i] != i + 1) 
                return i + 1;
        }

        // 特殊情况, nums = [1], 上面的循环不会返回结果，此时返回n + 1即可
        return n + 1;
    }
};

本题中，数的个数为n个，但数的范围不在[1, n]中。需要返回缺失的第一个正整数。虽然乍一看不完全符合上题总结的原地哈希法的使用条件，但加上限制条件的原地哈希法依然可以被应用于解决本题。

203.移除链表元素

本题不能这样写：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;

        for (ListNode* cur = dummyHead; cur != NULL; cur = cur->next)
        {
            if (cur->next != NULL && cur->next->val == val)
                cur->next = cur->next->next;
        }
        return dummyHead->next;
    }
};

这样写会导致删除节点后，cur 指针向后移动到了 cur->next->next，从而可能跳过了紧接着的需要删除的节点。比如：

1	1 -> 2 -> 2 -> 3, target = 2

上述写法会导致第三个节点2不能被删除。

本题应当用while循环写，对一个节点，如果是目标节点，则将其删除，否则，向后移动一个节点，不能同时既删除节点又后移一位。本题正确的代码如下所示：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;

        ListNode* cur = dummyHead;
        while (cur->next != NULL)
        {
            // 如果既删又后移，则会漏掉节点
            if (cur->next->val == val) cur->next = cur->next->next; // 要么删
            else cur = cur->next; // 要么后移
        }
        return dummyHead->next;
    }
};

本题的完整主函数：

#include <iostream>
using namespace std;

struct ListNode
{
    int val;
    ListNode* next;
    ListNode(int x): val(x), next(NULL) {}
};

ListNode* remove(ListNode* head, int val)
{
    ListNode* dummyHead = new ListNode(0);
    dummyHead->next = head;

    ListNode* cur = dummyHead;
    while (cur->next != NULL)
    {
        if (cur->next->val == val) cur->next = cur->next->next;
        else cur = cur->next;
    }

    return dummyHead->next;
}

int main()
{
    // head = [1,2,6,3]
    ListNode* node1 = new ListNode(1);
    ListNode* node2 = new ListNode(2);
    ListNode* node3 = new ListNode(6);
    ListNode* node4 = new ListNode(3);
    node1->next = node2;
    node2->next = node3;
    node3->next = node4;

    ListNode* head = remove(node1, 3);
    for (ListNode* cur = head; cur != NULL; cur = cur->next) cout << cur->val << ' ';
    cout << endl;
    return 0;
}

构造链表时，也可以采用函数写法：

#include <iostream>
using namespace std;

struct ListNode
{
    int val;
    ListNode* next;
    ListNode(int x): val(x), next(NULL) {}
};

ListNode* appendNode(ListNode*& head, int val)
{
    // 头为空，则将新节点作为头节点
    if (head == NULL) head = new ListNode(val);
    // 头不为空，则遍历到链表最后一个节点，将新节点添加到最后一个节点之后
    else
    {
        ListNode* cur = head;
        while (cur->next != NULL) cur = cur->next;
        cur->next = new ListNode(val);
    }
    return head;
}

ListNode* remove(ListNode* head, int val)
{
    ListNode* dummyHead = new ListNode(0);
    dummyHead->next = head;

    ListNode* cur = dummyHead;
    while (cur->next != NULL)
    {
        if (cur->next->val == val) cur->next = cur->next->next;
        else cur = cur->next;
    }

    return dummyHead->next;
}

int main()
{
    // head = [1,2,6,3]
    ListNode* node = NULL;
    appendNode(node, 1);
    appendNode(node, 2);
    appendNode(node, 6);
    appendNode(node, 3);

    ListNode* head = remove(node, 3);
    for (ListNode* cur = head; cur != NULL; cur = cur->next) cout << cur->val << ' ';
    cout << endl;
    return 0;
}

在定义链表时，特别要注意下面用来赋值的这句话：ListNode(int x): val(x), next(NULL) {}。

707.设计链表

本题的细节很多，需要特别注意。

// get函数的复杂写法
int get(int index) {
    if (index < 0 || index > _size - 1) return -1;

    LinkedList* cur = _dummyHead;
    index ++ ;
    while (cur != NULL)
    {
        cur = cur->next;
        index -- ;
        if (index == 0) break;
    }
    return cur->val;
}

本题的完整代码如下所示：

class MyLinkedList {
public:
    struct LinkedList
    {
        int val;
        LinkedList* next;
        LinkedList(int x): val(x), next(NULL) {}
    };

    MyLinkedList() {
        _dummyHead = new LinkedList(0);
        _size = 0;
    }
    
    int get(int index) {
        if (index < 0 || index > _size - 1) return -1;

        LinkedList* cur = _dummyHead->next;
        while (index -- ) cur = cur->next;
        return cur->val;
    }
    
    void addAtHead(int val) {
        LinkedList* head = new LinkedList(val);
        head->next = _dummyHead->next;
        _dummyHead->next = head;
        _size ++ ;
    }
    
    void addAtTail(int val) {
        LinkedList* tail = new LinkedList(val);
        LinkedList* cur = _dummyHead;
        while (cur->next != NULL) cur = cur->next;
        cur->next = tail;
        _size ++ ;
    }
    
    void addAtIndex(int index, int val) {
        if (index < 0 || index > _size) return;
        LinkedList* newNode = new LinkedList(val);
        LinkedList* cur = _dummyHead;
        while (index -- ) cur = cur->next;
        newNode->next = cur->next;
        cur->next = newNode;
        _size ++ ;
    }
    
    void deleteAtIndex(int index) {
        if (index < 0 || index > _size - 1) return;
        LinkedList* cur = _dummyHead;
        while (index -- ) cur = cur->next;
        cur->next = cur->next->next;
        _size -- ;
    }

private:
    LinkedList* _dummyHead;
    int _size;
};

注意事项：

带下划线的变量表示类中的变量，而非局部变量
记得在private中定义类中的变量
注意插入节点时先更新后面的边，再更新前面的边
别忘记_size ++ / _size —
注意对参数index进行判断
while (index -- ) cur = cur->next的意思是，首先判断index是否大于0，是，则index = index - 1，然后执行cur = cur->next

206.反转链表

我记得有递归写法，迭代写法，先尝试实现迭代写法，其本质是双指针。记住下面的图，即可写出本题的双指针法的代码：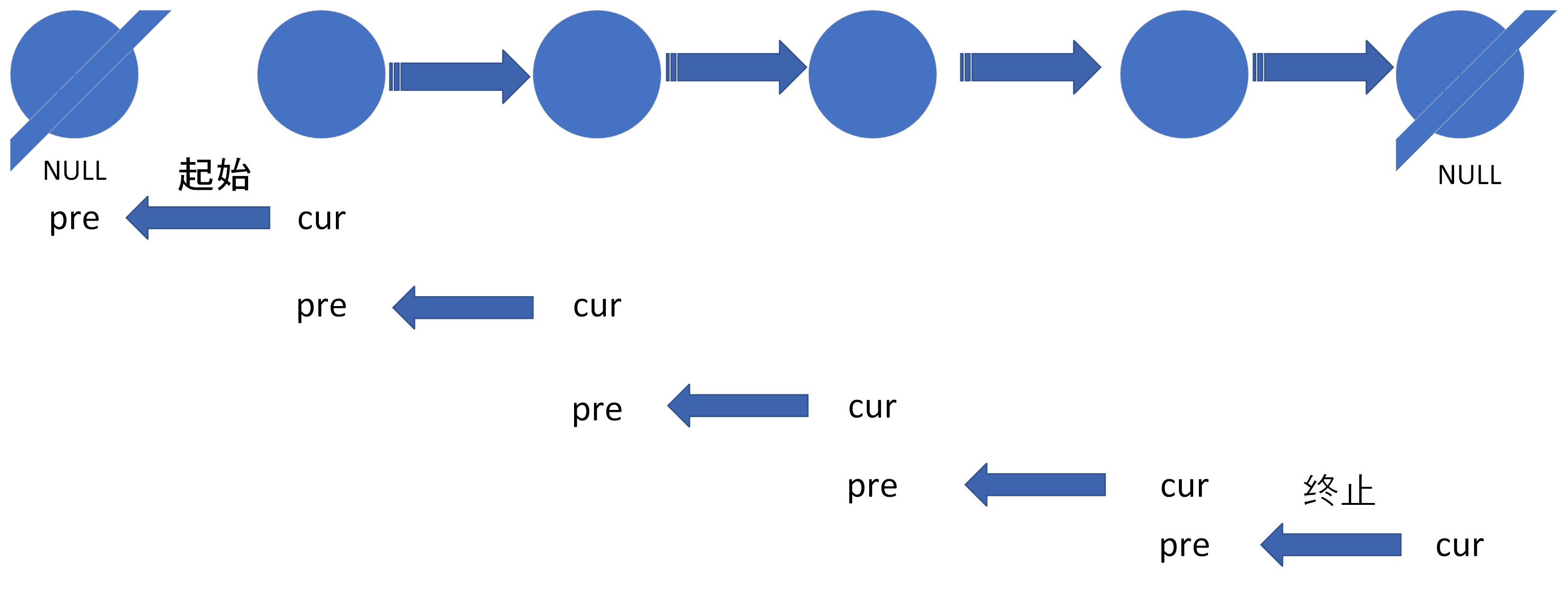

注意：pre从NULL开始，cur在NULL结束。

一个经典的错误：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = NULL;
        ListNode* cur = head;

        while (cur->next)
        {
            ListNode* tmp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = tmp;
        }
        return cur;
    }
};

这样写的结果是导致未将列表的最后一个节点（即反转后的头节点）的 next 指针正确设置。

本题的递归写法其实更加好写，但其空间复杂度为O(n)，高于双指针写法：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 终止条件
        if (head == NULL || head->next == NULL) return head;

        ListNode* last = reverseList(head->next);
        head->next->next = head;
        head->next = NULL;
        return last;
    }
};

24. 两两交换链表中的节点

首先尝试用双指针做法解决本题。直接看答案，记住本题的方法。其实不需要双指针，本题是一道单纯的模拟题，但要搞清楚循环终止条件。看过博客后，我写出了以下的代码：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* cur = dummyHead;
        
        // 终止条件：分别对应有偶数个节点和有奇数个节点
        while (cur->next && cur->next->next)
        {
            // 存1
            ListNode* tmp = cur->next;
            // 存3
            ListNode* tmp1 = cur->next->next->next;
            // d->2
            cur->next = cur->next->next;
            // 2->1
            cur->next->next = tmp;
            // 1->3
            tmp->next = tmp1;

            // 后移两位
            cur = cur->next->next;
        }
        return dummyHead->next;
    }
};

19.删除链表的倒数第N个节点

本题的笨办法：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* cur = dummyHead;

        int num = -1;
        // 计算节点数目
        while (cur)
        {
            cur = cur->next;
            num ++ ;
        }

        // 倒数第n个节点是正数第num - n个节点
        cur = dummyHead;
        while (num > n) // 不可以写成(num - n) -- 
        {
            cur = cur->next;
            num -- ;
        }
        cur->next = cur->next->next;
        return dummyHead->next;
    }
};

看博客，复习巧妙解法。本题的巧妙解法是快慢双指针。快指针先移动n位，然后快慢指针同时移动，直到快指针移动到链表的最后一个节点。此时，慢指针就指向了需要删除的节点。据此，我写出了本题的代码：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;

        ListNode* fast = dummyHead;
        ListNode* slow = dummyHead;
        // && fast可加可不加，因为本题有限制n<=链表长度，若无此限制，则必须加，否则会出现空指针异常
        while (n -- && fast) fast = fast->next;
        while (fast->next) 
        {
            fast = fast->next;
            slow = slow->next;
        }
        slow->next = slow->next->next;
        return dummyHead->next;
    }
};

也可以让快指针先移动n + 1步，然后快慢指针同时移动，直到快指针移动到链表的NULL节点。

160.相交链表

本题拿到我没什么思路，直接看以前的博客。本题的思路：首先计算两个链表的长度，将较长的链表作为链表a，较短的链表作为链表b。然后a链表从sizea - sizeb处开始, b链表从0处开始遍历，直到找到二者的交汇点。本质上体现的是一种末尾对齐的思想。示意图和代码如下所示：

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* cura = headA, *curb = headB;
        int sizea = 0, sizeb = 0;

        // 计算a的长度
        while (cura)
        {
            cura = cura->next;
            sizea ++ ;
        }

        // 计算b的长度
        while (curb)
        {
            curb = curb->next;
            sizeb ++ ;
        }

        // 让a为较长的链表, b为较短的链表
        if (sizea < sizeb)
        {
            swap(sizea, sizeb);
            swap(headA, headB);
            swap(cura, curb);
        }

        // a链表从sizea - sizeb处开始, b链表从0处开始
        cura = headA, curb = headB;
        int delta = sizea - sizeb;
        while (delta -- ) cura = cura->next;

        while (curb)
        {
            if (cura == curb) return cura;
            else 
            {
                cura = cura->next;
                curb = curb->next;
            }
        }
        return NULL;
    }
};

时间复杂度O(n + m)，空间复杂度O(1)。

142.环形链表II

我记得本题是用快慢指针解决的，快指针一次走两格，慢指针一次走一格，二者必然会在节点处相遇。我还记得公式怎么推导，但具体的思路记不清楚了，看博客。看完博客后，我写出了如下的代码：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head, * slow = head;
        
        // fast != NULL保证fast->next不报空指针异常
        // fast->next != NULL保证fast->next->next不报空指针异常
        while (fast && fast->next)
        {
            fast = fast->next->next;
            slow = slow->next;

            if (fast == slow)
            {
                ListNode* node1 = head, * node2 = fast;
                while (node1 != node2)
                {
                    node1 = node1->next;
                    node2 = node2->next;
                }
                return node1;
            }
        }
        return NULL;
    }
};

本题的思路：快慢指针必然会在环中的某处相交，且慢指针在进入环的第一圈中就会和快指针相交。记下交点，让一个指针从起点开始走，另一个指针从交点开始走，二者相交的位置就是环的入口。详细的数学推导和细节见博客。

时间复杂度O(n)，空间复杂度O(1)。

242.有效的字母异位词

本题简单，用数组做哈希，用数组统计一个字符串中各个字母出现的次数，然后遍历另一个字符串，在数组中做减减操作，最后判断数组中的所有元素是否都为0。我独立写出了本题的代码：

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;

        vector<int> hash(26, 0);

        for (int i = 0; i < s.size(); i ++ )
        {
            int tmp1 = s[i] - 'a';
            hash[tmp1] ++ ;
            int tmp2 = t[i] - 'a';
            hash[tmp2] -- ;
        }

        for (int i = 0; i < 26; i ++ )
        {
            if (hash[i]) return false;
        }
        return true;
    }
};

需要注意，数组的长度为26，而非s.size()，因为s和t中只含有26个英文字母。可以不用vector，用int类型的数组即可。

本题更简洁的版本的代码如下所示：

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;

        int hash[26] = {0};

        for (int i = 0; i < s.size(); i ++ )
        {
            hash[s[i] - 'a'] ++ ;
            hash[t[i] - 'a'] -- ;
        }

        for (int i = 0; i < 26; i ++ )
            if (hash[i]) return false;

        return true;
    }
};

349. 两个数组的交集

由于本题数据范围的限制，可以用数组做哈希，也可以用unordered_set做哈希。我首先写出了数组做哈希的写法（数组索引的范围与元素取值的范围相同），数组做哈希非常快：

数组哈希，数组去重

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        int hash1[1010] = {0};
        int hash2[1010] = {0};
        vector<int> res;

        for (int i = 0; i < nums1.size(); i ++ )
            hash1[nums1[i]] ++ ;
        
        for (int i = 0; i < nums2.size(); i ++ )
            hash2[nums2[i]] ++ ;
        
        for (int i = 0; i < 1010; i ++ )
        {
            if (hash1[i] && hash2[i]) res.push_back(i);
        }
        return res;
    }
};

尝试用unordered_set做本题。我不记得怎么用unordered_set做了，也忘记了unordered_set的基本做法，复习博客。

数组哈希，set去重

可以将数组和set结合，这样只需要一个数组即可完成本题：

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> res; // 用于结果集去重
        int hash[1010] = {0};

        for (int i = 0; i < nums1.size(); i ++ )
            hash[nums1[i]] ++ ;
        
        for (int i = 0; i < nums2.size(); i ++ )
            if (hash[nums2[i]]) res.insert(nums2[i]);
        
        return vector<int>(res.begin(), res.end());
    }
};

这里的set只是起到了去重的功能，没有起到哈希的功能，哈希的任务还是由数组承担了。注意如何将set转换为vector输出，直接vector<int> (res.begin(), res.end())。

set哈希，set去重

也可以完全用set做本题，set既用来做哈希，又用来去重，代码如下所示：

// 完全用set做本题
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> res;

        unordered_set<int> s1(nums1.begin(), nums1.end());

        for (int i = 0; i < nums2.size(); i ++ )
            if (s1.find(nums2[i]) != s1.end()) res.insert(nums2[i]);
            
        return vector<int> (res.begin(), res.end());
    }
};

202. 快乐数

我记得本题有个巧妙的做法。本题使用的数据结构应该是set。我直接看博客复习本题的写法。我错误的根本原因还是对本题的算法思路理解不清晰。在明确了思路后，我写下了如下的代码：

class Solution {
public:
    bool isHappy(int n) {
        unordered_set<int> s;

        while (1)
        {
            int sum = 0; // 用于存储各位数字的平方和

            while (n)
            {
                int digit = n % 10;
                sum += digit * digit;
                n = n / 10;
            }

            if (sum == 1) return true;
            if (s.find(sum) != s.end()) return false;
            n = sum;
            s.insert(sum);
        }
    }
};

本题的思路其实很简单，关键在于对平方和的计算和分类讨论（分为三类）。开一个死循环，计算n的各位数字的平方和。若平方和为1，则是快乐数。若平方和在set中出现过，则说明进入了死循环，不是快乐数。否则，将平方和加入到set中，将sum赋给n，进入下一重循环。

时间复杂度和空间复杂度都是O(logn)，详情参见博客。

1. 两数之和

本题要用map解决。用map的key存储索引，map的value存储nums中的值。首先将数组中的值依次存入map中，然后再在map中搜索target - nums[i]，若找到，则返回一对索引。本题思路我是清楚的，但由于忘了map的一些写法，因此复习博客。

实际上，我对本题的理解还是不够深刻。应该是用map的key存储数组中的值，map的value存储数组中的元素的下标，因为我们的目的是快速查找值是否出现过，被快速查找的对象应该被作为key。

先查再插

看完博客后，我写出了以下的代码：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> m;

        for (int i = 0; i < nums.size(); i ++ )
        {
            int t = target - nums[i];
            if (m.find(t) != m.end()) 
            {
                auto it = m.find(t);
                return {i, it->second};
            }
            m.insert({nums[i], i});
        }
        return {};
    }
};

本题的思路为：先查后插。先查现有的map中有无target - nums[i]，有，则将其索引和i一起加入结果集。无，则将遍历到的元素继续插入map中。这样天然的可以防止同一个元素被取出两次。

记住map的一些用法：

m.insert({nums[i], i})
m.find(key) != m.end()
auto it = m.find(t); int value = it->second;

插完再查

本题更复杂版本的代码，由于没有先查后插，导致要对找到的索引进行判断，其不能等于当前遍历到的索引，否则会导致同一个数字被使用了两次：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> m;

        for (int i = 0; i < nums.size(); i ++ )
            m.insert({nums[i], i});
        
        for (int i = 0; i < nums.size(); i ++ )
        {
            int t = target - nums[i];
            auto it = m.find(t);
            if (it != m.end() && it->second != i) return {i, it->second};
        }
        return {};
    }
};

压缩字符串（面试真题）

将aaaabb压缩为a4b2，将abcde保持原样不动。我独立写出了以下的代码，可以通过所有的测试样例：

#include <iostream>

using namespace std;

string compress(string s)
{
    if (s.size() == 1) return s;

    string res;
    char tmp = s[0];
    int size = 1;

    for (int i = 1; i < s.size(); i ++ )
    {
        res += tmp;
        while (i < s.size() && s[i] == s[i - 1]) 
        {
            i ++ ;
            size ++ ;
        }

        if (size > 1) res += to_string(size); // 也可以写成res += '0' + size;
        if (i < s.size()) tmp = s[i];
        size = 1;
    }

    // 处理最后一个字符
    if (s[s.size() - 1] != s[s.size() - 2]) res += s[s.size() - 1]; 

    return res;
}

int main()
{
    // 将aaabb转换为a3b2输出
    // 将abcde原样输出
    string s = "aaa";
    string res = compress(s);
    cout << res << endl;
}

其实没有必要在for循环中嵌套while循环，直接用一个for循环就可以搞定。以下的写法为推荐写法：

#include <iostream>
#include <string>

using namespace std;

// aaabb->a3b2
string compress(string s)
{
    if (s.size() == 0 || s.size() == 1) return s;

    string res;
    char tmp = s[0];
    int size = 1;

    for (int i = 1; i < s.size(); i ++ )
    {
        // 出现相同字母
        if (s[i] == s[i - 1]) size ++ ;
        // 出现不同字母
        else
        {
            // 将上一个字符和其出现次数（>1）插入res中
            res += tmp;
            if (size > 1) res += to_string(size);
            // 恢复现场
            tmp = s[i];
            size = 1;
        }
    }

    // 处理字符串的最后一位
    res += tmp;
    if (size > 1) res += to_string(size);

    return res;
}

int main()
{
    string s = "aaaanbv";
    string res = compress(s);
    cout << res << endl;
}

本题的关键在于分两种情况讨论：出现相同的字母/出现不同的字母，最后记得处理字符串的最后一位

通过本题，记住常用操作——将数字转换为字符：to_string(size)

可以写出上述操作的逆过程的代码：

#include <iostream>
#include <string>

using namespace std;

bool isdigit(char s)
{
    if (s >= '0' && s <= '9') return true;
    return false;
}

string decompress(string s)
{
    string res;

    // s的第一个元素必为字母，从第二个元素开始可能为数字
    // 一对对处理，先处理字母，再处理数字（可能有，也可能没有）
    for (int i = 0; i < s.size(); i ++ )
    {
        // 处理字母
        char tmp = s[i];

        // 处理数字，计算count
        int count = 0;
        while (i + 1 < s.size() && isdigit(s[i + 1])) 
        {
            count = count * 10 + s[i + 1] - '0';
            i ++ ;
        }

        // 字母加入结果集
        if (count == 0) res += tmp;
        // 若有数字，则将字母重复数字遍
        else while (count -- ) res += tmp; // 也可调用函数res.append(count, tmp);
    }
    return res;
}

int main()
{
    string s = "a56b12";
    string res = decompress(s);
    cout << res << endl;
}

本题的关键在于字母和数字成对出现（当然数字可能没有），成对地处理字母和数字，将它们成对地放入res中。

454.四数相加II

本题用哈希做的时间复杂度应该为O(n^2)。先枚举nums1和nums2中所有元素之和的组合，然后再在nums3和nums4中查找所有元素之和为-nums1[i] - nums2[j]的情况。由于涉及到索引，所以要用map，map的key存数值，map的value存索引。value似乎要存一组索引，比如(i, j)，我忘记怎么写了，看下博客。

实际上，应该是用map的key存储和，map的value存储出现这个和的次数。据此，我写出了以下的代码：

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        unordered_map<int, int> m;

        for (int i = 0; i < nums1.size(); i ++ )
            for (int j = 0; j < nums2.size(); j ++ )
                m[nums1[i] + nums2[j]] ++ ;

        int count = 0;
        for (int i = 0; i < nums3.size(); i ++ )
        {
            for (int j = 0; j < nums4.size(); j ++ )
            {
                if (m.find(-nums3[i] - nums4[j]) != m.end()) 
                    count += m.find(-nums3[i] - nums4[j])->second;
            }
        }
        return count;
    }
};

更简洁的写法：

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        unordered_map<int, int> m;

        for (int num1: nums1)
            for (int num2: nums2)
                m[num1 + num2] ++ ;
        
        int count = 0;
        for (int num3: nums3)
            for (int num4: nums4)
                if (m.find(-num3 - num4) != m.end())
                    count += m[-num3 - num4];

        return count;
    }
};

注意：

用map的key存储和，map的value存储出现这个和的次数
map的key不可重复，map的value可以重复。本题中的map起到一个将相同的和归拢，并用value统计其出现次数的作用
cpp中的map中的value是支持++操作的，且value可以通过key直接索引到，就像普通的数组那样
时间和空间复杂度均为$O(n^2)$，空间复杂度为$O(n^2)$是两数组的数字各不相同，产生了$n^2$种组合。

383. 赎金信

本题用数组做哈希就可以，因为对象就是26个小写英文字母。据此，我写出了以下的代码：

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        int cnt[26] = {0};

        for (int i = 0; i < magazine.size(); i ++ )
            cnt[magazine[i] - 'a'] ++ ;
        
        for (int i = 0; i < ransomNote.size(); i ++ )
            cnt[ransomNote[i] - 'a'] -- ;
        
        for (int num: cnt)
            if (num < 0) return false;
        return true;
    }
};

终极优化版本：

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        int cnt[26] = {0};

        // Each letter in magazine can only be used once in ransomNote
        if (ransomNote.size() > magazine.size()) return false;

        for (char m: magazine)
            cnt[m - 'a'] ++ ;

        for (char r: ransomNote)
        {
            cnt[r - 'a'] -- ;
            if (cnt[r - 'a'] < 0) return false;
        }
        return true;
    }
};