Day 29 Leetcode 491, 46, 47

链接

491.递增子序列
46.全排列
47.全排列 II

知识

491.递增子序列

46.全排列

47.全排列 II

初次尝试

491.递增子序列

本题的关键：递增、至少两个元素、去重。但本题存在一个很大的问题，就是去重的时候不能对原数组进行排序，否则会打乱原数组的顺序，以以下测试样例为例：

Input: nums = [4,4,3,2,1]
Output: [[4,4]]

一旦顺序被打乱，实际输出和理论输出就会不同，会多出很多递增的子序列。

本题和90.子集II非常像，但又很不一样，很容易掉坑里。直接看卡尔的讲解吧。

46.全排列

本题是排列问题，不需要startIndex，但我写不出代码，直接看卡尔的讲解。经过卡尔的提示用used数组避免重复取元素后，我独立写出了以下的代码：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, vector<int>& used)
    {
        // 终止条件
        if (path.size() == nums.size())
        {
            res.push_back(path);
            return;
        }

        // 单层递归逻辑
        for (int i = 0; i < nums.size(); i ++ )
        {
            if (used[i] == 1) continue;
            // 处理节点
            path.push_back(nums[i]);
            used[i] = 1;
            // 递归
            backtracking(nums, used);
            // 回溯
            path.pop_back();
            used[i] = 0;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<int> used(nums.size(), 0);
        backtracking(nums, used);
        return res;
    }
};

47.全排列 II

本题中的数组中会有重复元素，因此本题需要去重逻辑。本题相当于40.组合总和II去重逻辑和46.全排列的结合。我先尝试用set去重。我独立写出了以下的代码：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, vector<int>& used)
    {
        // 终止条件
        if (path.size() == nums.size())
        {
            res.push_back(path);
            return;
        }

        unordered_set<int> uset;
        for (int i = 0; i < nums.size(); i ++ )
        {
            if (uset.find(nums[i]) != uset.end() || used[i] == 1) continue;
            // 处理节点
            uset.insert(nums[i]);
            used[i] = 1;
            path.push_back(nums[i]);
            // 递归
            backtracking(nums, used);
            // 回溯
            used[i] = 0;
            path.pop_back();
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<int> used(nums.size(), 0);
        backtracking(nums, used);
        return res;
    }
};

再接着尝试写出used数组去重的代码。我独立写出了如下的代码：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, vector<int>& used)
    {
        // 终止条件
        if (path.size() == nums.size())
        {
            res.push_back(path);
            return;
        }

        for (int i = 0; i < nums.size(); i ++ )
        {
            if (used[i] == 1 || i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;
            // 处理节点
            used[i] = 1;
            path.push_back(nums[i]);
            // 递归
            backtracking(nums, used);
            // 回溯
            used[i] = 0;
            path.pop_back();
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<int> used(nums.size(), 0);
        sort(nums.begin(), nums.end());
        backtracking(nums, used);
        return res;
    }
};

由于本题中nums[i]的数据范围在-10-10之间，所以可以不用set去重，而是用数组去重（将数据范围-10-10映射到数组下标范围0-20），这样效率更高，代码如下所示：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, vector<int>& used)
    {
        // 终止条件
        if (path.size() == nums.size())
        {
            res.push_back(path);
            return;
        }

        // 数组去重
        int hash[21] = {0};

        for (int i = 0; i < nums.size(); i ++ )
        {
            if (used[i] == 1 || hash[nums[i] + 10]) continue;
            // 处理节点
            hash[nums[i] + 10] = 1;
            used[i] = 1;
            path.push_back(nums[i]);
            // 递归
            backtracking(nums, used);
            // 回溯
            used[i] = 0;
            path.pop_back();
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<int> used(nums.size(), 0);
        backtracking(nums, used);
        return res;
    }
};

实现

491.递增子序列

列出递增子序列，子序列元素数量大于等于2。有以下测试样例：

Input: [4, 7, 6, 7]
Output: [4, 7, 7], [4, 7], [4, 6], [4, 6, 7], [6, 7], [7, 7]

要求不能有重复的子序列，因此需要去重。本题和90.子集II，只不过要求元素有顺序，且元素个数大于等于2。实际上，本题的细节和90有很大区别。本题的去重思路不可以沿用先排序再去重的做法，因为会改变原数组中元素的顺序，导致递增子序列的改变。例如对上述测试样例排序后，递增子序列会包括[4, 6, 7, 7]，实际上原本的输出不包含[4, 6, 7, 7]。

所有的回溯算法都是深搜，所有的深搜都可以说是递归。画本题的树形结构：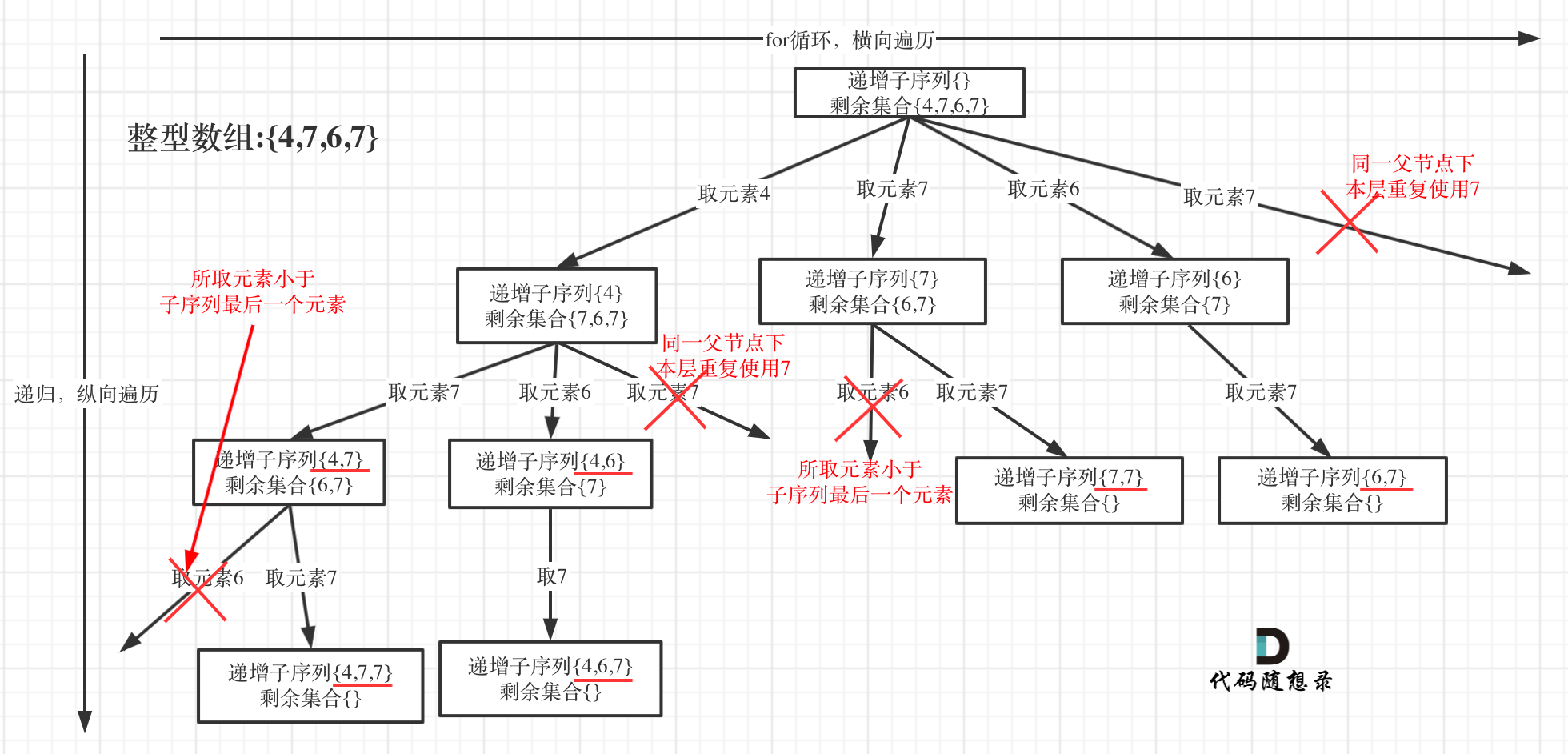

去重为树层去重。现在开始写代码：

vector<int> path; // 单个结果
vector<vector<int>> res; // 结果集

void backtracking(vector<int>& nums, int startIndex)
{
    // 子集类问题可以不写终止条件，具体原因参见78/90
    if (path.size() >= 2) res.push_back(path); // 子集中元素数量大于等于2
    
    unordered_set<int> uset; // set去重
    
    // 单层递归逻辑
    for (int i = startIndex; i < nums.size(); i ++ )
    {
        // 剪枝条件1：所取元素小于子序列最后一个元素，此时要求子序列非空，否则path.back()会报错
        // 剪枝条件2：用set做树层去重
        if (!path.empty() && nums[i] < path.back() || uset.find(nums[i]) != uset.end()) continue;
        
        // 处理节点
        // 记录每一层取的数(for循环中除去递归部分外都是横向遍历的)，每一层不能重复取相同的数
        uset.insert(nums[i]); 
        path.push_back(nums[i]);
        // 递归
        backtracking(nums, i + 1);
        // 回溯
        path.pop_back();
    }
}

为什么没有对uset做回溯操作？
原因：上述代码中，每进入一层递归，都会重新定义一个uset。因此uset就是确保同一层中没有取到相同的元素，在进入下一层递归时，uset会被刷新。因此uset并不会对树枝去重，只会对树层去重。而used数组需要做回溯，因为used数组记录的是元素是否在path中被使用过，因此path中加减元素都需要对used数组进行修改。

本题的去重方式也可以应用于40.组合总和II和90.子集II。本题也可以用数组取代set进行去重，用数组的效率会更高些。

本题的完整代码如下所示：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, int startIndex)
    {
        // 收集结果
        if (path.size() >= 2) res.push_back(path);
        unordered_set<int> uset;

        // 单层递归逻辑
        for (int i = startIndex; i < nums.size(); i ++ )
        {
            // 剪枝条件1：所取元素小于子序列最后一个元素，此时要求子序列非空，否则path.back()会报错
            // 剪枝条件2：用set做树层去重
            // cpp中&&的优先级高于||，因此是先与后或，不需要给剪枝条件1加括号
            if (!path.empty() && nums[i] < path.back() || uset.find(nums[i]) != uset.end()) continue;
            // 处理节点
            uset.insert(nums[i]);
            path.push_back(nums[i]);
            // 递归
            backtracking(nums, i + 1);
            // 回溯
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums, 0);
        return res;
    }
};

由于本题nums[i]的数据范围很小，因此可以用数组做去重，运行效率也更高。只需要将set替换为普通数组，然后做一个偏移（数值-100-100映射到数组下标0-200上）即可。代码如下所示：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    void backtracking(vector<int>& nums, int startIndex)
    {
        if (path.size() > 1) res.push_back(path);
        int cnt[201] = {0};

        for (int i = startIndex; i < nums.size(); i ++ )
        {
            if (!path.empty() && nums[i] < path.back() || cnt[nums[i] + 100] == 1) continue;
            cnt[nums[i] + 100] = 1;
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }

    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums, 0);
        return res;
    }
};

46.全排列

题目中明确说了给定的集合中没有重复元素，因此不用去重。

排列相对于组合的区别：[2, 1], [1, 2]是同一个组合，但是两个排列。排列是强调元素顺序的，组合不强调元素顺序。接下来画本题的树形结构。

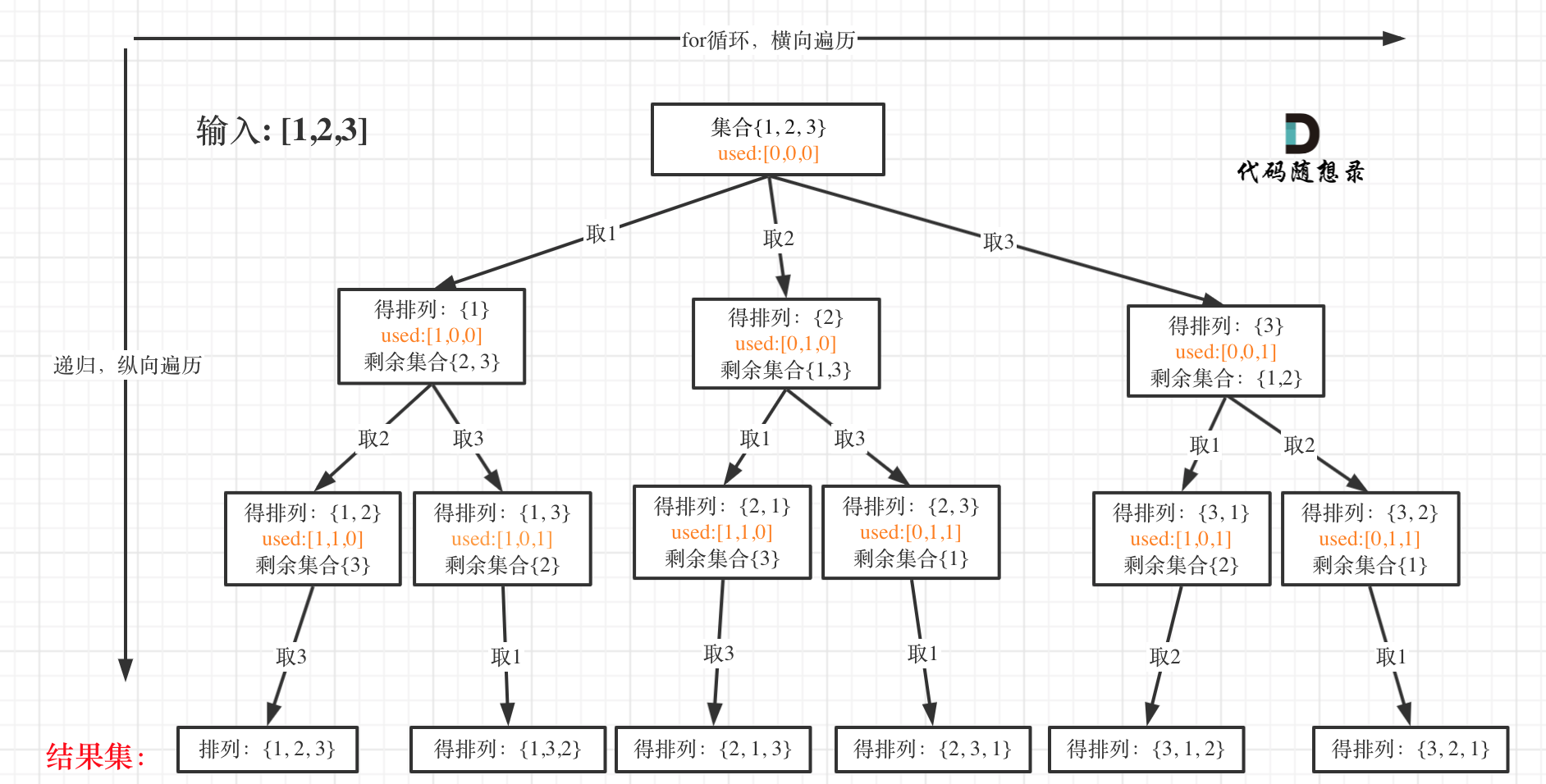
排列问题中也需要用到used数组，用于标记哪些元素被使用过，因为在排列问题中同一个元素不能重复使用。组合问题中是用startIndex来避免取同一个元素和避免产生相同组合的情况。树的深度由nums的长度来控制。

used数组用来标记哪些元素被取过，取过的元素不能重复取，但所有没取过的元素都可以重复取，而不需要像组合问题那样用startIndex来控制只能取当前元素的下一个元素。具体的代码如下所示：

vector<int> path; // 放单个结果
vector<vector<int>> res; // 结果集

void backtracking(vector<int>& nums, vector<int>& used)
{
    // 终止条件
    if (path.size() == nums.size())
    {
        res.push_back(path); // 收获结果
        return;
    }
    
    // 单层递归逻辑
    // 排列问题不需要startIndex，只要不重复取同一个元素即可
    for (int i = 0; i < nums.size(); i ++ )
    {
        if (used[i] == 1) continue; // 不重复取同一个元素
        // 处理节点
        used[i] = 1;
        path.push_back(nums[i]);
        // 递归
        backtracking(nums, used);
        // 回溯
        used[i] = 0;
        path.pop_back();
    }
}

47.全排列 II

上一题给定的集合中没有重复元素，本题给定的集合中有重复元素。以[1, 1, 2]为例，如果依然用上一题的办法求解本题，结果集中会出现两个[1, 1, 2]，因此本题需要做去重。如果对去重的思路不够了解，可以看40.组合总和II。回溯的所有题目中，去重的逻辑都是相同的。本题等于排列+去重。但排列问题中的去重会有些与之前不同的地方。

画出本题的树形结构：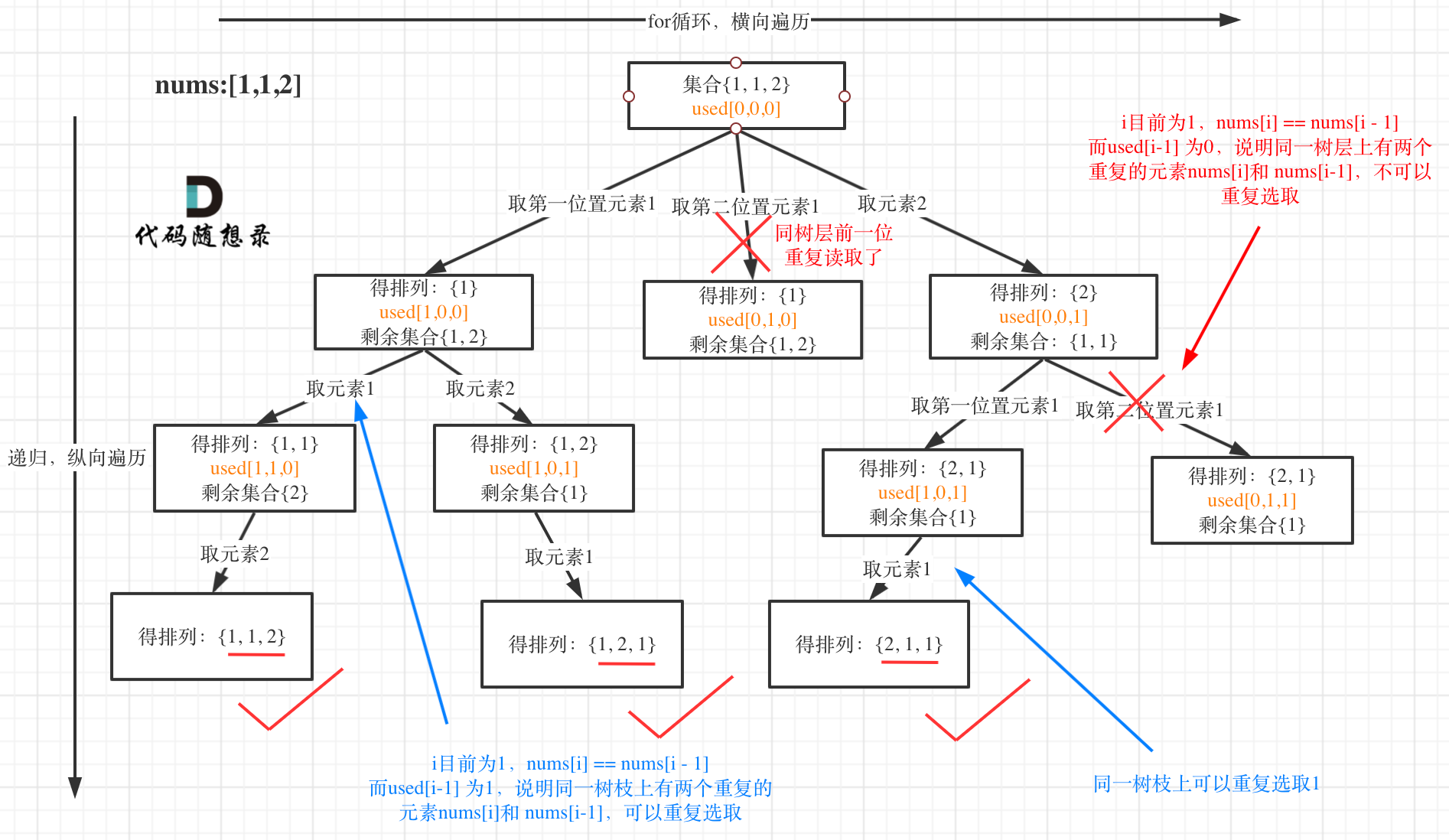

用used数组做树层去重前，记得对nums数组进行排序。本题中的used数组有两个作用：

• 避免同一个元素被重复使用
• 做树层去重

接下来写具体的代码：

vector<int> path;
vector<vector<int>> res;

void backtracking(vector<int>& nums, vector<int>& used)
{
    // 终止条件
    if (path.size() == nums.size())
    {
        res.push_back(path);
        return;
    }
    
    // 单层递归逻辑
    for (int i = 0; i < nums.size(); i ++ )
    {
        // 树层去重
        if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;
        // 同一个元素不能被重复取，因此取过的数直接跳过
        if (used[i] == 1) continue;
        
        // 处理节点
        used[i] = 1;
        path.push_back(nums[i]);
        // 递归
        backtracking(nums, used);
        // 回溯
        used[i] = 0;
        path.pop_back();
    }
}

细节：

// 树层去重
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) continue;

可以通过

// 树枝去重
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 1) continue;

也可以通过。这意味着树层去重和树枝去重都可以解决本题。但树层去重的效率更高，树层去重会剪掉更多分支，而树枝去重要一直到最后一个树枝才会列出所有的结果。因此还是推荐树层去重的写法。以[1, 1, 1]为例，画出树层去重和树枝去重的树形结构：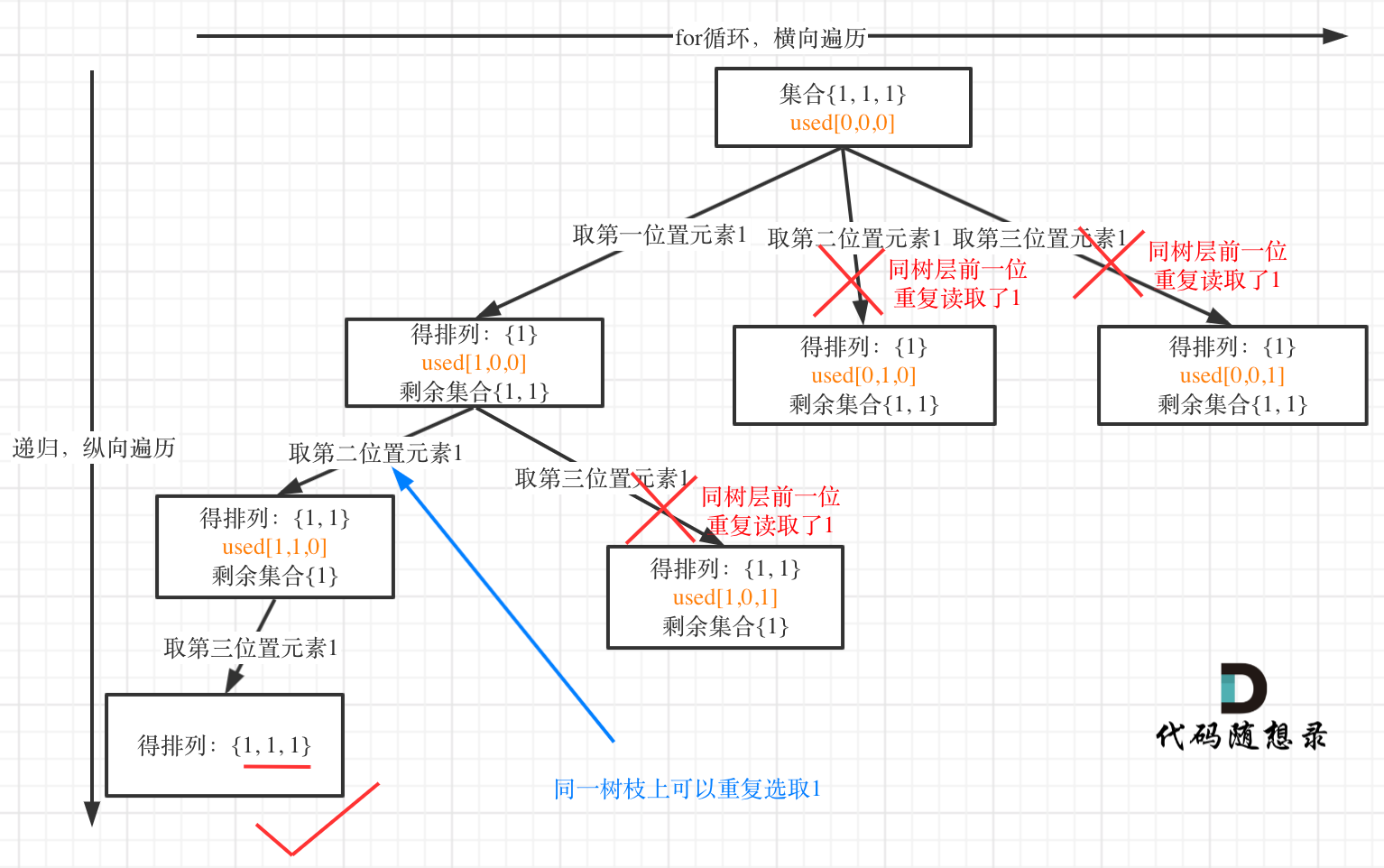

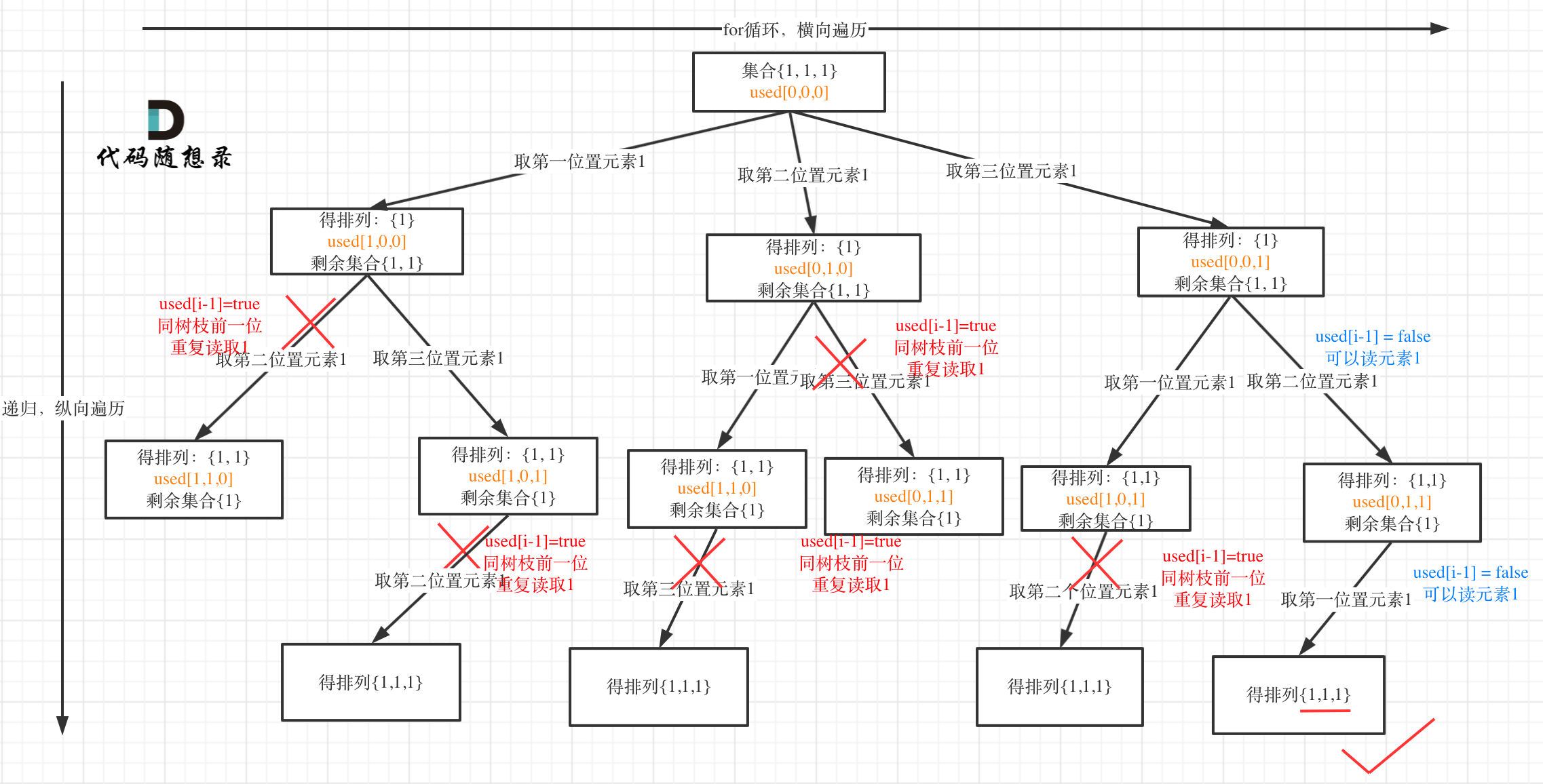
很清晰的看到，树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索。

时间复杂度和空间复杂度分析：

• 时间复杂度: 最差情况所有元素都是唯一的，时间复杂度为$O(n!\times n)$。 对于n个元素一共有n!中排列方案。而对于每一个答案，我们需要$O(n)$去复制最终放到res数组。
• 空间复杂度: $O(n)$。空间复杂度即为回溯树的深度，其取决于nums数组中有多少个元素。

心得与备忘录

491.递增子序列

关键点：set去重->剪枝->数组去重取代set去重

1. 本题和90.子集II乍一看非常相似，但细节上有很大不同，解决本题时不能有惯性思维。

2. 之前去重的方法都是利用used数组，这意味着需要对nums数组进行排序。在本题中，如果对nums数组进行排序，就会打乱原数组中元素的顺序，导致递增子序列发生改变。因此，本题不能用used数组去重，而需要用set去重。因为用set去重不需要对原数组排序。

3. 本题有两个剪枝条件：

   • 剪枝条件1：若所取元素小于子序列最后一个元素，则需要剪枝。此时要求子序列非空，否则path.back()会报错。剪枝条件1的原因是本题要求子序列是递增的。

   • 剪枝条件2：用set做树层去重

   两个剪枝条件用||相连。

4. 为什么不需要对set进行回溯？

   每进入一层递归，都会重新定义一个set。因此set就是确保同一层中没有取到相同的元素。在进入下一层递归时，set会被刷新（重新定义）。因此set并不会对树枝去重，只会对树层去重。而used数组需要做回溯，因为used数组记录的是元素是否在path中被使用过，因此path中加减元素都需要对used数组进行相应的修改。

5. 本题的去重方法也可以应用于40.组合总和II和90.子集II。

6. 由于本题nums[i]的数据范围很小，因此可以用数组做去重，运行效率也更高。只需要将set替换为普通数组，然后做一个偏移（数值-100-100映射到数组下标0-200上）即可。

7. 本题的时间和空间复杂度分别为$O(n\times2^n)$和$O(n)$。同90和78。

46.全排列

1. 排列问题和组合问题的两大区别：
   • 每层都是从0开始搜索而不是startIndex
   • 需要used数组记录path里都放了哪些元素了
2. 不需要startIndex的原因：[1, 2]和[2, 1]是同一个组合，但却是不同的排列，因此排列问题不能像组合问题那样从当前元素的下一个元素开始取，而是要取nums数组中所有当前没有取过的元素。
3. 需要used数组的原因：used数组记录了此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。
4. 终止条件为path.size() == nums.size()，nums数组的大小限制了树的深度。
5. 本题的时间复杂度为$O(n!)$，空间复杂度为$O(n)$。时间复杂度的原因是有$n$个元素的nums数组共有$n!$种排列。空间复杂度的原因是递归的深度（即树的深度）为$n$。

47.全排列 II

1. 本题相当于40.组合总和II（树层去重）和46.全排列的结合。
2. 本题的去重有三种写法：set去重、数组去重、used数组去重。三种写法我都在初次尝试中给出了。
3. 用used数组去重前，一定要记得对nums数组进行排序。另外两种去重写法则不需要对nums数组进行排序。
4. 由于本题是在叶子节点处收集结果，因此需要终止条件。
5. 本题的时间复杂度为$O(n!\times n)$，空间复杂度为$O(n)$。具体原因参见实现部分。
6. 本题用树层去重和树枝去重都可以，具体原因参见实现部分。但树层去重的效率远高于树枝去重，因此采用一贯以来的used数组树层去重写法即可，不要纠结树枝去重的原理和合理性。