Day 30 Leetcode 332, 51, 37

链接

332.重新安排行程
51. N皇后
37. 解数独
总结

知识

51. N皇后

初始化一个vector<string>，其中的元素全是字符.（共有n行，每行是一个字符串，每个字符串由n个.构成）：

vector<string> chessboard(n, string(n, '.'));

实现

今天这三道题都非常难，那么这么难的题，为啥一天做三道？

因为一刷也不求能把这么难的问题解决，所以一刷的时候，就了解一下题目的要求，了解一下解题思路，不求能直接写出代码，先大概熟悉一下这些题，二刷的时候，随着对回溯算法的深入理解，再去解决如下三题。

332.重新安排行程

本题的思路不难，但选择的数据结构和初始化、遍历等操作非常复杂，是一道难题。

本题需要一个特殊的数据结构来存储一个机场映射多个机场，机场之间要靠字母序排列的这种复杂关系，选择的数据结构是unordered_map<string, map<string, int>> targets。其具体的含义为unordered_map<出发机场, map<到达机场, 航班次数>> targets。在遍历 unordered_map<出发机场, map<到达机场, 航班次数>> targets的过程中，可以使用”航班次数”这个字段的数字做相应的增减，来标记到达机场是否使用过了。如果“航班次数”大于零，说明目的地还可以飞，如果“航班次数”等于零说明目的地不能飞了，而不用对集合做删除元素或者增加元素的操作。有如下代码：

// unordered_map<出发机场, map<到达机场, 航班次数>> targets
// 使用map的原因是为了让其key有序（字典序）
// 第一个unordered_map是为了存储出发机场和到达机场间的映射关系，第二个map是为了对到达机场按照字典序排序，且记录到达机场在输入数据中出现的次数
unordered_map<string, map<string, int>> targets;

本题的树形结构如下所示，以输入：[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例：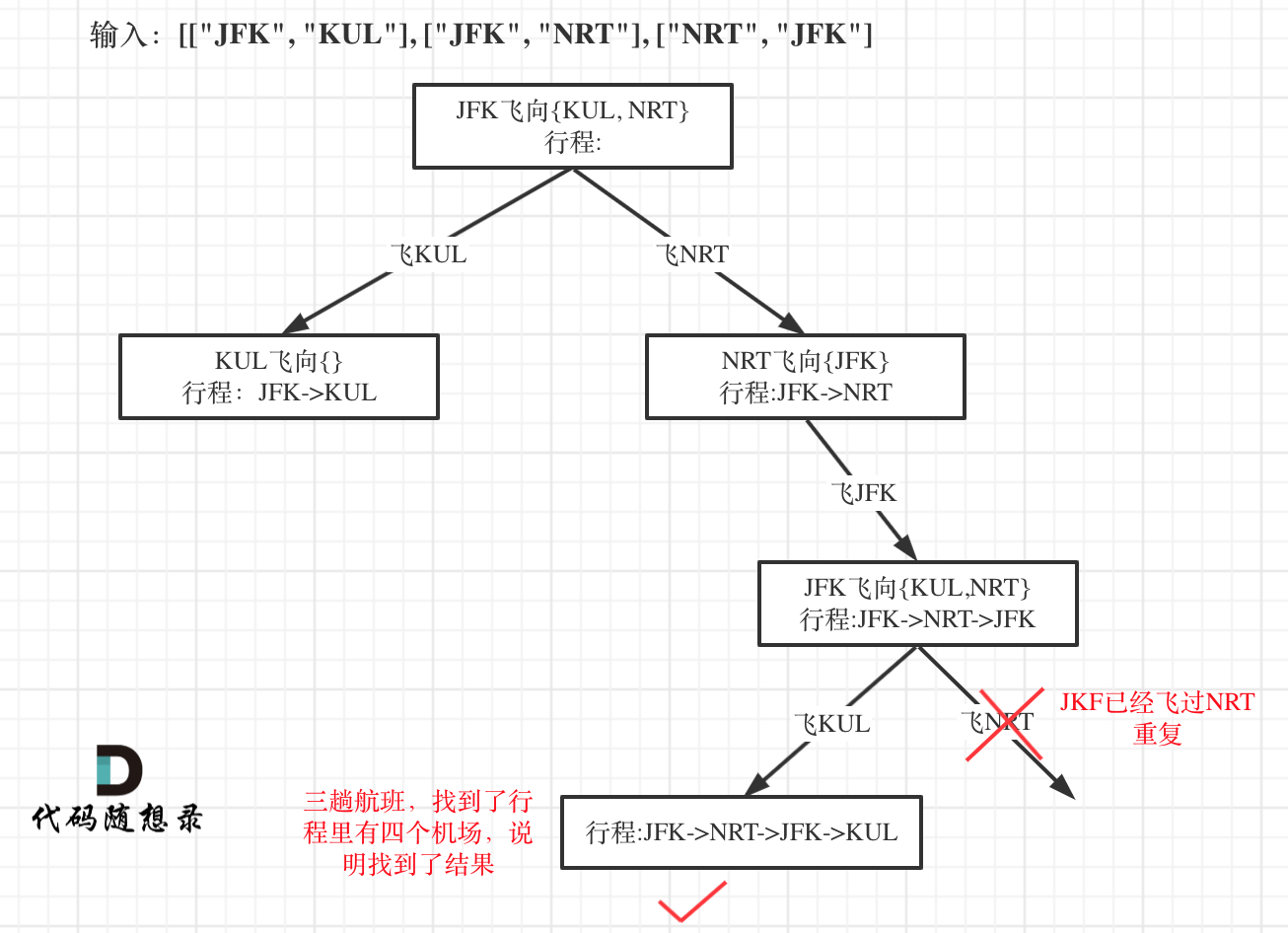

对上述树形结构的解释：始终从JFK出发，输入中JFK可以到KUL或者NRT，因此可以有这两个选择。输入中没有以KUL作为出发点的航班，因此飞向KUL的那一枝结束。飞向NRT的一枝，输入中以NRT为出发点的航班的终点是JFK，因此有行程：JFK->NRT->JFK。输入中以JFK为出发点的航班的终点可以是KUL或者NRT，因此分为两枝。JKF已经飞过NRT，因此剪枝；JKF飞KUL构成了行程：JFK->NRT->JFK->KUL，三趟航班，形成中有四个机场，说明找到了结果。

通过上述分析，我们可以得出代码的终止条件：n张机票，即有n个航班，则行程中有n + 1个机场（机场可重复）时，收集结果。原因是行程是由若干个向量组成的，每个向量都是一个航班，行程是单向的，不会形成环。因此，若有n个向量（即n个航班），那么就会有n + 1个节点（即单个向量的首尾），即n + 1个机场。有如下代码：

vector<string> res; // 存放结果，即由n个航班拼接成的行程，其中有n + 1个机场

// ticketNum为票数，即航班数
if (result.size() == ticketNum + 1) {
    return true;
}

在写单层递归逻辑前，需要先对res数组和targets数组进行初始化，代码如下所示：

for (const vector<string>& vec : tickets) {
    targets[vec[0]][vec[1]]++; // 记录映射关系
}
result.push_back("JFK"); // 起始机场

tickets数组是输入，其类型是vector<vector<string>>。由于输入不可更改，且其中的每个元素的类型都是vector<string>，因此用类型为const vector<string>的变量对其进行遍历，这里的引用就不加都可以，不会影响运行结果。vec[0]为出发机场，vec[1]为到达机场。targets中存储的是出发机场与到达机场的映射关系。对一个出发机场，若输入中存在其的到达机场，则在targets中记录这个映射关系，且map<string, int>中的string存储到达机场（vec[1]），int存储次数（有出发机场和其对应的到达机场，则该int存1）。这实现了对每一个航线（从某个出发机场到某个目的地机场）的航班次数进行计数。

根据树形结构，可以写出单层递归的逻辑：

for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
    if (target.second > 0 ) { // 记录到达机场是否飞过了
        result.push_back(target.first);
        target.second--;
        if (backtracking(ticketNum, result)) return true;
        result.pop_back();
        target.second++;
    }
}

这里特别需要注意的是：

for (pair<const string, int>& target : targets[result[result.size() - 1]])

其含义为：result[result.size() - 1] 获取 result 向量的最后一个元素，即当前路径中最新的机场。然后，使用这个机场名称作为键，从 targets 映射中检索对应的内层 map，这个内层 map 包含所有从该机场出发的航班及其次数。for 循环遍历这个内层 map，即遍历从当前结果集中的最新机场可以直接到达的所有机场及对应的航班次数。一定要加上引用即 & target，因为后面有对 target.second 做减减操作，如果没有引用，单纯复制，这个结果就没记录下来，那最后的结果就不对了。加上引用之后，就必须在string前面加上const，因为map中的key是不可修改了，这就是语法规定了。

还需要注意本题的递归函数的返回值和参数：

bool backtracking(int ticketNum, vector<string>& result)

注意函数返回值用的是bool！因为我们只需要找到一个行程，就是在树形结构中唯一的一条通向叶子节点的路线。所以找到了这个叶子节点了直接返回。

拆分地写好了各部分的代码之后，整合起来就是本题的完整代码：

class Solution {
public:
    unordered_map<string, map<string, int>> targets;

    bool backtracking(int ticketSum, vector<string>& res)
    {
        // 终止条件
        if (ticketSum + 1 == res.size()) return true;

        // 单层递归逻辑
        // 以res中最新机场为出发点，遍历targets寻找可能的目的地
        for (pair<const string, int>& target: targets[res[res.size() - 1]])
        {
            // target.second > 0说明目的地可用
            if (target.second > 0) 
            {
                // 处理节点
                res.push_back(target.first);
                target.second -- ;
                // 递归
                if (backtracking(ticketSum, res)) return true;
                // 回溯
                res.pop_back();
                target.second ++ ;
            }
        }
        return false;
    }

    vector<string> findItinerary(vector<vector<string>>& tickets) {
        // 初始化res
        vector<string> res;
        res.push_back("JFK"); 

        // 初始化targets
        for (auto vec: tickets)
            targets[vec[0]][vec[1]] ++ ;

        // 调用递归函数并返回结果
        backtracking(tickets.size(), res);
        return res;
    }
};

使用auto来简化上述代码，避免需要手写复杂的变量类型：

class Solution {
public:
    // 提取输入数据中的信息：构造出发机场和到达机场间的映射，到达机场按照字典序排序并记录到达机场出现的次数
    unordered_map<string, map<string, int>> targets;

    bool backtracking(int ticketSum, vector<string>& res)
    {
        // 终止条件
        if (ticketSum + 1 == res.size()) return true;

        // 单层递归逻辑
        for (auto& target: targets[res[res.size() - 1]])
        {
            if (target.second > 0)
            {
                target.second -- ;
                res.push_back(target.first);
                if (backtracking(ticketSum, res)) return true;
                target.second ++ ;
                res.pop_back();
            }
        }
        return false;
    }

    vector<string> findItinerary(vector<vector<string>>& tickets) {
        // 初始化res
        vector<string> res;
        res.push_back("JFK");
        // 初始化targets
        for (auto ticket: tickets) targets[ticket[0]][ticket[1]] ++ ;
        backtracking(tickets.size(), res);
        return res;
    }
};

51. N皇后

本题是回溯中较难的题目。题意：给一个n*n的棋盘，在其中放n个皇后，要求同一行、同一列、同意斜线上不能有两个皇后，将放置皇后的结果返回。难点：之前讲的组合问题、分割问题、子集问题和排列问题，都是一个一维的集合按照条件输出若个子集，本题则是一个二维的集合（数组）。

首先想如何暴力枚举，以4*4的棋盘为例，需要4个for循环，每一行每个位置尝试放皇后，根据规则判断能否放皇后。回溯算法的本质和暴力枚举没有区别，但回溯算法用递归的方式控制嵌套for循环的层数。

本题的树形结构如下所示，以3*3的棋盘为例：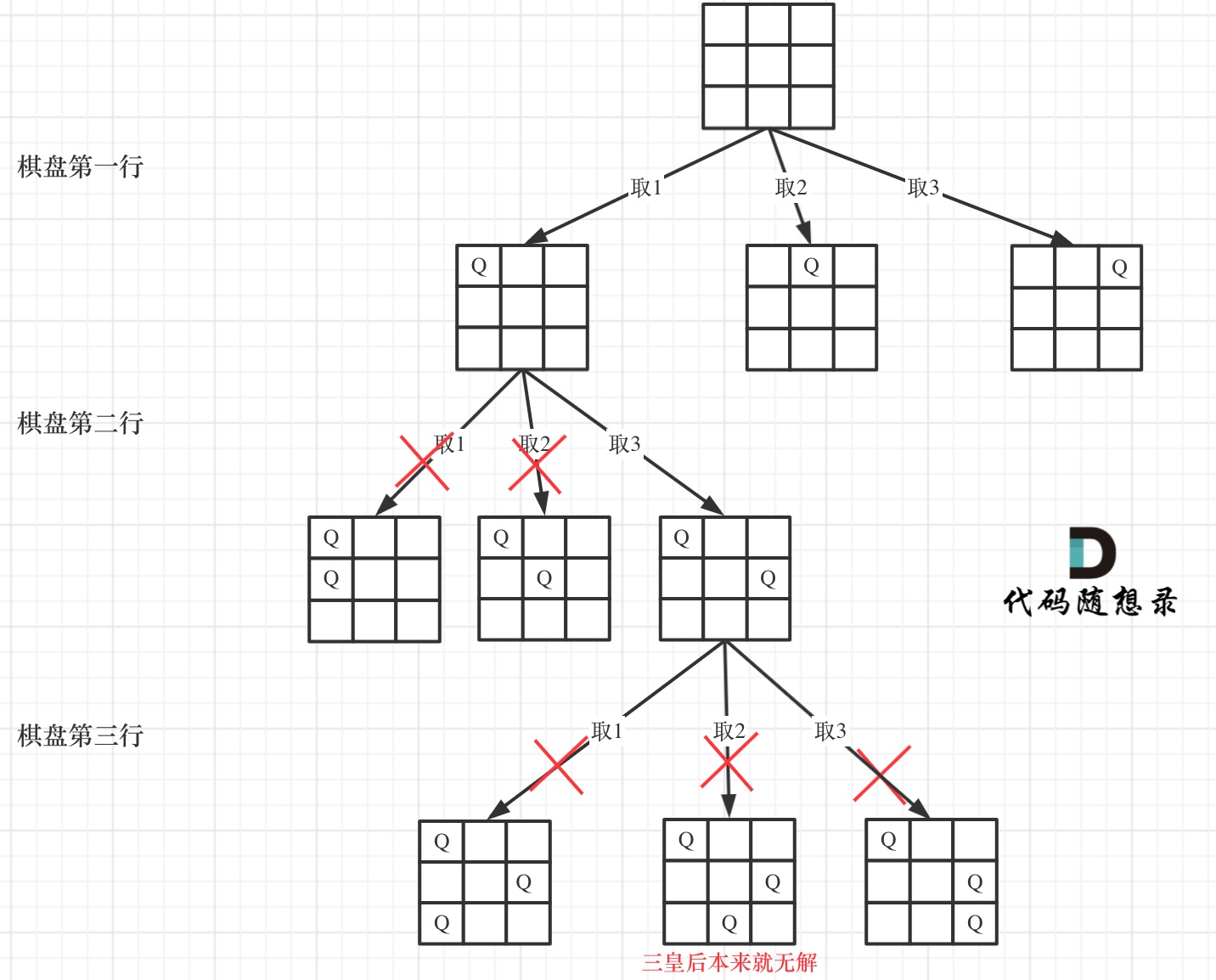

第n层递归对应着尝试在第n行中放置皇后。3*3的N皇后问题是无解的，画其只是为了展现其树形结构。树的深度为棋盘的行数，树的宽度为棋盘的列数。接下来写本题的代码：

// 每个棋盘是一个二维数组，放置若干棋盘，因此需要三维数组
vector<vector<vector<int>>> res; // 三维数组收集所有可能的摆放结果

// chessboard为棋盘，n为棋盘的大小, row为行，第n层递归负责处理第n行，用row来记录当前处理到了第几行
void backtracking(vector<vector<int>> chessboard, int n, int row)
{
    // 终止条件: 叶子节点收获结果
    if (row == n) 
    {
        res.push_back(chessboard); // 单层递归逻辑中会对合法性进行判断，保证放入res中的chessboard都是合法的
        return;
    }
    
    // 单层递归逻辑
    for (int i = 0; i < n; i ++ )
    {
        // 合法性判断
        // 判断在第row行，第i个位置放皇后是否合法
        if (isValid(row, i, chessboard, n))
        {
            // 放皇后
            chessboard[row][i] = 'Q'; 
            // 递归
            backtracking(chessboard, n, row + 1); // 下一层递归, row->row + 1
            // 回溯
            chessboard[row][i] = '.';
        }
    }
}

总结：回溯法解决二维数组问题，第n层递归处理第n行，每层递归中遍历每一行中的每个元素。

在理解了本题的主题思路后，独立写出代码依然有难度，因为本题返回的变量类型是vector<vector<string>，chessboard的变量类型应该为vector<string>，对其进行初始化有一定难度。另外，isValid函数的实现我第一次写也有一定的困难，直接看文字版讲解。

我独立写出的本题的代码如下：

class Solution {
public:
    // 结果集
    vector<vector<string>> res;

    bool isValid(vector<string>& chessboard, int n, int row, int col)
    {
        // 同一列中不能有两个皇后
        for (int i = 0; i < row; i ++ )
            if (chessboard[i][col] == 'Q') return false;

        // 主对角线不能有两个皇后
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i -- , j -- )
            if (chessboard[i][j] == 'Q') return false;

        // 副对角线不能有两个皇后
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i -- , j ++ )
            if (chessboard[i][j] == 'Q') return false;

        return true;
    }

    // 传入棋盘，棋盘大小，行数（即递归层数）
    void backtracking(vector<string>& chessboard, int n, int row)
    {
        // 终止条件
        if (row == n) 
        {
            res.push_back(chessboard);
            return;
        }

        // 单层递归逻辑
        for (int i = 0; i < n; i ++ )
        {
            // 合法性判断
            if (isValid(chessboard, n, row, i))
            {
                // 放皇后
                chessboard[row][i] = 'Q';
                // 递归
                backtracking(chessboard, n, row + 1);
                // 回溯
                chessboard[row][i] = '.';
            }
        }
    }

    vector<vector<string>> solveNQueens(int n) {
        vector<string> chessboard(n, string(n, '.'));
        backtracking(chessboard, n, 0);
        return res;
    }
};

需要特别注意的是，在放皇后时，每次只在一行中的某个位置放一个皇后，且放完后会回溯，因此同一行中不会出现两个皇后，因此不需要在isValid函数中对同一行中出现两个皇后的情况进行判断。另外，放皇后的顺序是从行数小放到行数大，从列数小放到列数大。在不同行中，行数小的位置会被优先尝试放置皇后。在同一行的不同列中，列数小的位置会被优先尝试放置皇后。因此，isValid函数中对同一列判断，只需要判断从0-row列；对主对角线判断，只需要判断i从row-1到0，j从col-1到0；对副对角线判断，只需要判断i从row - 1到0，j从col + 1到n（由于优先放小的行，所以i < row, j > col的位置可能已经放置了皇后）。

37. 解数独

给一个99的棋盘，用1-9填满这个棋盘，规则为：同一行中不能有重复的数字，同一列中不能有重复的数字，九宫格中不能有重复的数字。本题求出一个填满的方案即可。本题是回溯章节的难题，和上一题N皇后类似。但用N皇后的思路做本题做不出来。*本题比N皇后多一个维度。N皇后用for循环遍历行，递归遍历列。本题不仅行要放满数字，列也要放满数字，整个棋盘都要放满数字。

本题解法被称为二维递归，即两个for循环，下面是一个递归函数。一个for循环来遍历行，一个for循环来遍历列，这样才能确定一个空格。递归用来确定空格中应该放的数字。本题的树形结构如下所示：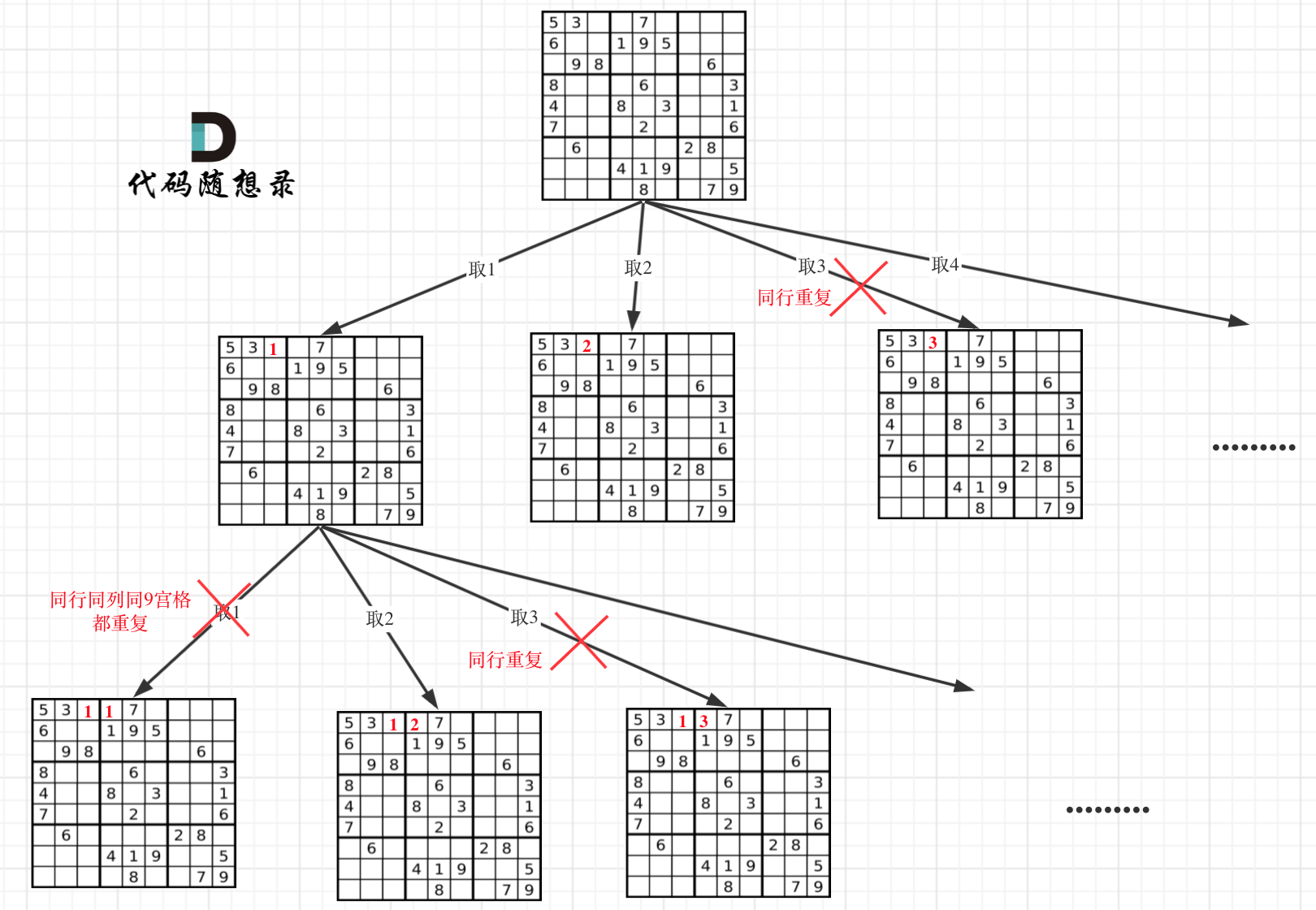

现在开始写本题的代码，本题的代码其实并不复杂。

// 确定递归函数的返回值和参数
// 返回值为bool类型，原因是本题求数独的一个解即可，一旦棋盘被填满，立即返回
// 若一题有多个结果，多个结果散落在树形结构里，需要将树形结构全都搜索一遍，然后将结果放入结果集中，因此返回值为void类型
bool backtracking(vector<vector<char>>& board) // board要引用，这样才会修改board
{
    // 本题不需要写终止条件，棋盘被填满后会直接return true，若无法满足填充规则，则会return false
    // 两个for循环，一个遍历行，另一个遍历列
    for (int i = 0; i < board.size(); i ++ )
        for (int j = 0; j < board[0].size(); j ++ )
        {
            // 处理节点
            // 棋盘中的点表示空格
            if (board[i][j] == '.')
            {
                for (char k = '1'; k <= '9'; k ++ )
                {
                    // 检查在board的(i, j)处放置数字k是否合法
                    if (isValid(i, j, k, board)) 
                    {
                        board[i][j] = k;
            					 // 进入下一层递归
                        bool res = backtracking(board);
                        // 找到一个结果就立即停止搜索，返回
                        if (res == true) return true;
                        // 回溯
                        board[i][j] = '.';
                    }
                }
                return false; // 在空格处将9个数字都尝试了，无法填入，则说明该棋盘没有结果，返回false
            }
        }
    // 若没有走到return false，则return true（若棋盘一直被填充直到被填满，则不会走if (board[i][j] == '.')）
    return true; 
}

根据上面的核心代码，我自己实现了isValid函数，写出了本题的完整代码：

class Solution {
public:
    bool isValid(int i, int j, char k, vector<vector<char>>& board)
    {
        // 检查第i行能否放入k
        for (int j = 0; j < board[0].size(); j ++ )
            if (board[i][j] == k)
                return false;

        // 检查第j列能否放入k
        for (int i = 0; i < board.size(); i ++ )
            if (board[i][j] == k)
                return false;
        
        // 检查九宫格能否放入k
        int starti = i / 3 * 3;
        int startj = j / 3 * 3;
        int endi = starti + 2;
        int endj = startj + 2;
        for (int i = starti; i <= endi; i ++ )
            for (int j = startj; j <= endj; j ++ )
                if (board[i][j] == k)
                    return false;

        return true;
    }

    bool backtracking(vector<vector<char>>& board)
    {
        for (int i = 0; i < board.size(); i ++ )
            for (int j = 0; j < board[0].size(); j ++ )
            {
                if (board[i][j] == '.')
                {
                    // 处理节点
                    for (char k = '1'; k <= '9'; k ++ )
                    {
                        if (isValid(i, j, k, board))
                        {
                            board[i][j] = k;
                            // 递归
                            bool res = backtracking(board);
                            if (res == true) return true;
                            // 回溯
                            board[i][j] = '.';
                        }
                    }
                    return false;
                }
            }
        return true;
    }

    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};

心得与备忘录

332.重新安排行程

1. 本题的解题思路其实不难，画出树形结构后，是一道经典的回溯问题。本题的难点在于选用怎样的数据结构来有效地存放和处理输入的数据。
2. 因为本题是hard题，且由于使用了较为复杂的数据结构，因此我觉得在hard中都算是难题，显著比N皇后困难。因此，第一遍学习本题，了解本题的思路和核心代码即可，不要求能够将本题完整地写出来。

3. 本题的实现部分对代码进行了细致的拆分讲解，大致可以分为以下几个要点：

   • 用怎样的数据结构存储输入数据中出发机场和到达机场间的映射关系，且要求同一个出发机场的到达机场按照字典序排列，同时记录到达机场的使用次数
   • 如何对结果集和上面的数据结构进行初始化
   • 根据树形结构写出终止条件和单层搜索逻辑，并确定递归函数的返回值和传入的参数。本题递归函数的返回值是罕见的bool类型，而非void类型

   明确上述三个问题，即可理解本题的思路和实现细节，进而顺畅地写出本题的代码。

4. 在初始化targets时，范围遍历可以直接采用auto类型的变量，避免需要手写复杂的变量类型。但在单层递归逻辑中遍历targets时，不能直接采用auto，因为for循环中涉及到了对遍历的值的修改操作，因此一定要使用引用，可以使用auto&。

51. N皇后

1. 本题的新奇之处在于：之前用回溯法解决过组合、切割、子集、排列问题，处理的对象都是一维数组，N皇后问题处理的对象却是二维数组。

2. 本题的原理实际上非常简单，理解本题的树形结构即可：

   

3. 由上述树形结构可知，树的宽度是棋盘的列数，树的深度是棋盘的行数。据此，可以轻松地写出backtracking函数的终止条件和单层递归逻辑。

4. 对棋盘合法性的判断其实是比较容易写错的。按照以下标准验证棋盘是否合法，两皇后：

   • 不能同行

   • 不能同列

   • 不能同斜线 （主对角线和副对角线）

   在isValid函数中，不能同行的判断不需要写。因为在单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，且后序还会回溯释放掉这个元素。因此只需要写不能同列、不能同主对角线、不能同副对角线的判断。这三个判断的书写依据如下图所示。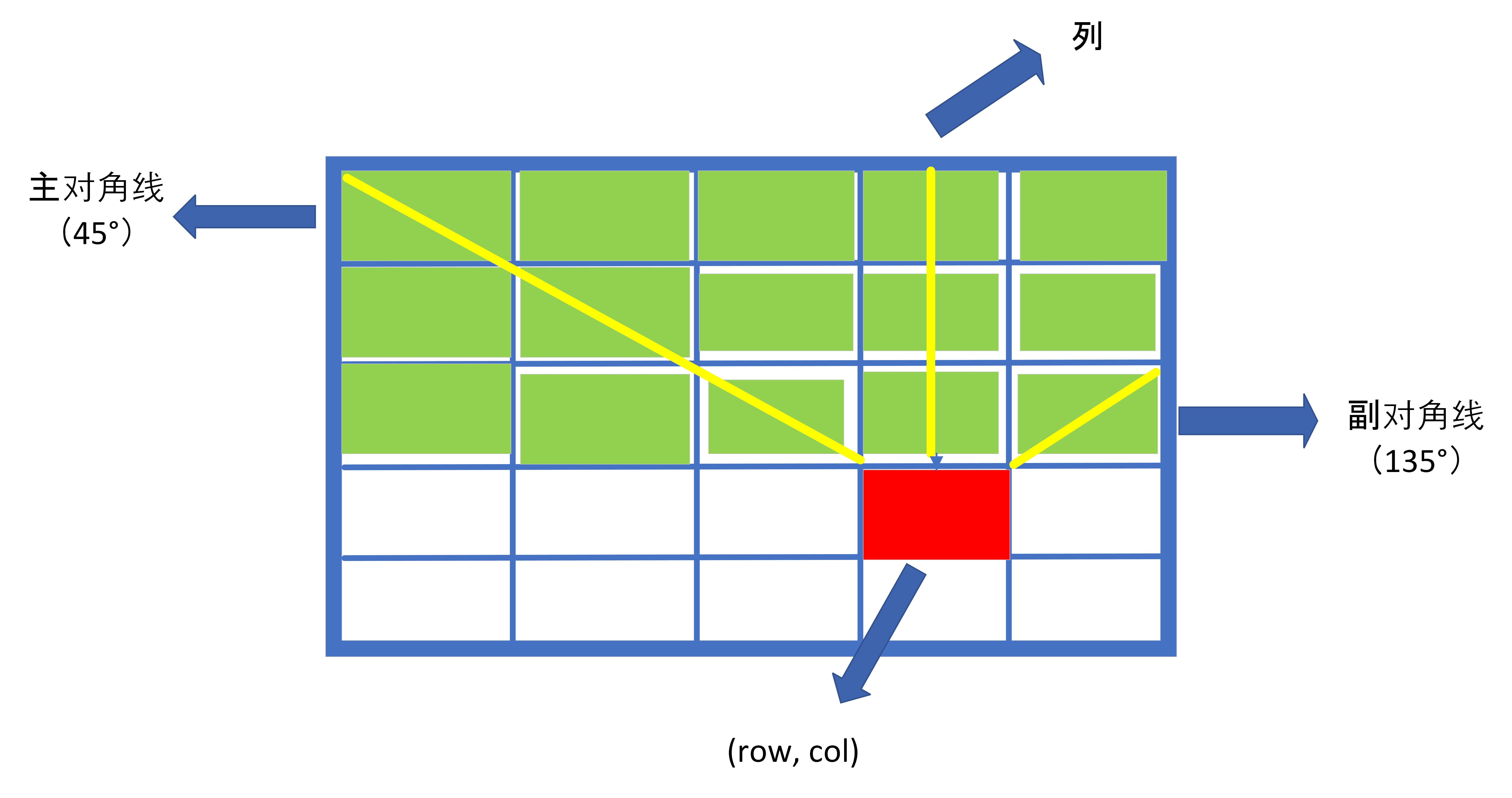

   

   当我们尝试在(row, col)处放置皇后时，只有绿色部分可能在之前被放置过皇后。原因是：递归到当前层，只有行数<row的格点上可能被放置过皇后。根据三条黄线，可以方便地写出三个判断。

5. 本题的时间复杂度O(n!)，空间复杂度O(n)。

   • 时间复杂度：由于回溯法的本质依然是暴搜，因此，在棋盘的第一行，有n种放置皇后的方式；第二行最多有n - 1种，依次类推，得到时间复杂度为O(n!)。
   • 空间复杂度即为树的深度，即为棋盘的行数，故空间复杂度为O(n)。

37. 解数独

1. 和之前的递归题目不同，本题的递归是二维递归。一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，一行一列确定下来之后，递归遍历这个位置放9个数字的可能性。
2. 本题递归函数的函数返回值类型为bool类型。原因是本题只需要找到一个解，就立即返回。如果需要搜索整棵二叉树，找到所有的解，然后将结果记录在结果集中，那么递归函数的返回值类型为void。
3. 本题不需要写终止条件。因为在递归逻辑中，如果找到了满足条件的解，就会直接return true。如果某个空格中无论填入哪个数字都无法满足条件，就会直接return false。
4. 注意return true和return false的位置。前者放在递归函数末尾，意思是若棋盘一直被填充直到被填满，则不会走if (board[i][j] == '.')，就return true。后者放在for (char k = '1'; k <= '9'; k ++ )的结束之处，意思是在空格处将9个数字都尝试了，无法填入，则说明该棋盘没有结果，return false。
5. 时间复杂度：O(9^m) , m是’.’的数目。空间复杂度：$O(n^2)$，原因是递归的深度是n^2（原因是第一层for循环代表树的宽度，后面两层for循环代表了树的深度。由于本题中数独的长宽固定为9，因此本题中的n = 9）。
6. 回溯的题目到此结束，总体来说比较简单，有统一的模板，但每个题目又有一些需要注意的小细节。